Разрезающий циклы набор рёбер

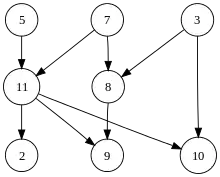
В теории графов ориентированный граф может содержать ориентированные циклы, кольцо дуг, имеющих одно направление. В некоторых приложениях такие циклы нежелательны, мы можем исключить их и получить направленный ациклический граф (Directed Acyclic Graph, DAG). Один из способов исключения дуг — просто удаление дуг из графа. Разрезающий циклы набор дуг (Feedback Arc Set, FAS) или разрезающий циклы набор рёбер — это множество дуг, которые, при удалении их из графа, образуют DAG. Рассматривая под другим углом, это множество, содержащее по меньшей мере одно ребро из каждого цикла графа.

Этот ориентированный граф не имеет циклов — невозможно прийти в любую вершину обратно в ту же точку по дугам в направлениях, указанных стрелками.

Тесно связанным понятием является разрезающее циклы множество вершин, в которое входит по меньшей мере по одной вершине из каждого цикла ориентированного графа, и минимальное остовное дерево, которое является неориентированным вариантом задачи нахождения разрезающего циклы набора дуг.

Минимальный разрезающий циклы набор дуг (который нельзя уменьшить в размере удалением рёбер) имеет дополнительное свойство, что если в нём рёбра заменить на обратные, а не удалить, граф остаётся ациклическим. Нахождение небольшого множества рёбер с таким свойством является ключевым шагом в послойном рисунке графа [1][2].

Иногда желательно отбросить как можно меньше дуг, образуя наименьший разрезающий циклы набор дуг, или двойственный наибольший ациклический подграф. Задача является сложной вычислительной задачей, для которой были разработаны некоторые аппроксимирующие решения.

Пример

В качестве простого примера представим следующую гипотетическую ситуацию, в которой для получения чего-то нужно что-то предпринять:

  • Ваша цель — получить газонокосилку.
  • Гарри говорит, что он даст газонокосилку, но только в обмен на микроволновку.
  • Джейн говорит, что она даст микроволновку, но только в обмен на пианино.
  • Джордж говорит, что он даст пианино, но только в обмен на газонокосилку.

Мы можем выразить эту ситуацию в виде задачи на графе. Пусть каждая вершина представляет предмет, и мы добавляем дугу из A в B, если мы должны иметь A, чтобы получить B. К несчастью, у вас нет ни одной из этих трёх вещей, а поскольку граф циклический, вы не можете ни одну из вещей получить.

Однако предположим, что вы даёте Джорджу $100 за его пианино. Если он их примет, это удалит дугу из газонокосилки к пианино. Таким образом, цикл разорван и вы можете сделать два обмена для получения желанной газонокосилки. Эта одна дуга составляет разрезающий циклы набор дуг.

Наименьший разрезающий циклы набор дуг

Как в примере выше, обычно с разрывом дуги связывается некоторая цена. По этой причине желательно удалить как можно меньше дуг. Удаление одной дуги достаточен для разрыва простого цикла, но в общем случае определение наименьшего числа дуг для удаления является NP-трудной задачей, а называется задачей наименьшего разрезающего циклы набора дуг или наибольшего ацикличного подграфа.

Теоретические результаты

Эта задача, в частности, трудна для рёберно k-связных графов для больших k, где каждая дуга оказывается во многих различных циклах. Задача в варианте разрешимости, являющаяся NP-полной, спрашивает, можно ли разрезать все циклы путём удаления не более k дуг. Эта задача входит в список 21 NP-полных задач Карпа[3][4].

Будучи NP-полной, задача нахождения разрезающего циклы набора дуг является фиксированно-параметрически разрешимой — существует алгоритм её решения, время работы которого зависит полиномиально от размера входного графа (но не зависящее от числа рёбер), но время экспоненциально зависит о числа рёбер в разрезающем циклы наборе дуг[5].

Вигго Канн (Viggo Kann) показал в 1992-ом, что задача поиска минимального разрезающего циклы набора дуг является APX -сложной, что означает, что существует константа c, такая, что, в предположении P≠NP, не существует полиномиального по времени аппроксимационный алгоритм, который всегда находит множество рёбер максимум в c раз большее, чем оптимальное[6][7]. К 2006-у году наибольшее значение c, для которого известно, что такого алгоритма нет, равно c = 1,3606[8]. Лучший из известных аппроксимационных алгоритмов имеет оценку O(log n log log n)[7][9]. Для двойственной задачи приближенного вычисления числа рёбер в ацикличном подграфе возможен алгоритм с коэффициентом чуть лучшим 1/2[10][11].

Если входные орграфы ограничены турнирами, задача известна под названием minimum feedback arc set problem on tournaments (задача нахождения разрезающего циклы набора дуг на турнирах, FAST). Эта ограниченная задача позволяет приближенную схему полиномиального времени и это утверждение остаётся верным для ограниченной взвешенной версии задачи[12]. Алгоритм с фиксированным субэкспоненциальным параметром для взвешенной FAST был предложен Карпинским и Шуди[13].

С другой стороны, если рёбра неориентированы, задача удаления рёбер для достижения графа без циклов эквивалентна нахождению минимального остовного дерева, что можно легко сделать за полиномиальное время.

Приближения

Были разработаны для задачи некоторые аппроксимационные алгоритмы[14]. Очень простой алгоритм следующий:

  • Фиксируем случайную перестановку вершин, то есть пронумеруем из от 1 до n.
  • Строим два подграфа, L и R, содержащие рёбра (u, v), при этом для первого графа u < v, для второго — u > v.

Теперь как L, так и R являются ациклическими подграфами графа G, и по меньшей мере один из этих графов по не более чем вдвое меньше максимального ациклического подграфа[15].

Примечания
  1. Di Battista, Eades, Tamassia, Tollis, 1998, с. 265–302.
  2. Bastert, Matuszewski, 2001, с. 87–120.
  3. Karp, 1972, с. 85–103.
  4. Garey, Johnson, 1979, с. 198.
  5. Chen, Liu, Lu, O'Sullivan, Razgon, 2008.
  6. Kann, 1992.
  7. Crescenzi, Kann, Halldórsson, Karpinski, Woeginger, 2000.
  8. Irit, Safra, 2005, с. 439–485.
  9. Even, Naor, Schieber, Sudan, 1998, с. 151–174.
  10. Berger, Shor, 1990, с. 236–243.
  11. Eades, Lin, Smyth, 1993, с. 319–323.
  12. Kenyon-Mathieu, Schudy, 2007, с. 95–103.
  13. Karpinski, Schudy, 2010, с. 3–14.
  14. Hassin, Rubinstein, 1994, с. 133–140.
  15. Skiena, 2010, с. 348; 559–561.

Литература
  • Giuseppe Di Battista, Peter Eades, Roberto Tamassia, Ioannis G. Tollis. Graph Drawing: Algorithms for the Visualization of Graphs. — Prentice Hall, 1998. — С. 265–302. — ISBN 9780133016154.
  • Oliver Bastert, Christian Matuszewski. Drawing Graphs: Methods and Models / Michael Kaufmann, Dorothea Wagner. — Springer-Verlag, 2001. — Т. 2025. — С. 87–120. — (Lecture Notes in Computer Science). — doi:10.1007/3-540-44969-8_5.
  • Richard M. Karp. Complexity of Computer Computations. — New York: Plenum,, 1972. — С. 85–103. — (Proc. Sympos. IBM Thomas J. Watson Res. Center, Yorktown Heights, N.Y.).
  • Michael R. Garey, David S. Johnson. Computers and Intractability: A Guide to the Theory of NP-Completeness. — W.H. Freeman, 1979. — ISBN 0-7167-1045-5.
  • Jianer Chen, Yang Liu, Songjian Lu, Barry O'Sullivan, Igor Razgon. A fixed-parameter algorithm for the directed feedback vertex set problem // Journal of the ACM. — 2008. — Т. 55, вып. 5. — doi:10.1145/1411509.1411511.
  • Viggo Kann. On the Approximability of NP-complete Optimization Problems. — Department of Numerical Analysis and Computing Science, Royal Institute of Technology, Stockholm, 1992.
  • Pierluigi Crescenzi, Viggo Kann, Magnús Halldórsson, Marek Karpinski, Gerhard J. Woeginger. A compendium of NP optimization problems. — 2000.
  • Dinur Irit, Shmuel Safra. On the hardness of approximating minimum vertex cover // Annals of Mathematics. — 2005. — Т. 162, вып. 1. — С. 439–485. — doi:10.4007/annals.2005.162.439.
  • G. Even, J. Naor, B. Schieber, M. Sudan. Approximating minimum feedback sets and multicuts in directed graphs // Algorithmica. — 1998. — Т. 20, вып. 2. — С. 151–174. — doi:10.1007/PL00009191.
  • B. Berger, P. Shor. Proceedings of the 1st ACM-SIAM Symposium on Discrete Algorithms (SODA’90). — 1990. — С. 236–243.
  • P. Eades, X. Lin, W. F. Smyth. A fast and effective heuristic for the feedback arc set problem // Information Processing Letters. — 1993. — Т. 47. — С. 319–323. — doi:10.1016/0020-0190(93)90079-O.
  • Claire Kenyon-Mathieu, Warren Schudy. Proc. 39th ACM Symposium on Theory of Computing (STOC '07). — 2007. — С. 95–103. — doi:10.1145/1250790.1250806.
  • M. Karpinski, W. Schudy. Proc. 21st ISAAC (2010). — 2010. — Т. 6506. — С. 3–14. — (Lecture Notes in Computer Science). — doi:10.1007/978-3-642-17517-6_3.
  • Refael Hassin, Shlomi Rubinstein. Approximations for the maximum acyclic subgraph problem // Information Processing Letters. — 1994. — Т. 51, вып. 3. — С. 133–140. — doi:10.1016/0020-0190(94)00086-7.
  • Steven Skiena. The Algorithm Design Manual. — 2nd. — Springer Science+Business Media, 2010. — ISBN 1-849-96720-2.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.