Птоон

Птоон[1][2] (Птой, греч. Πτώον) — низкие горы в Греции, в Беотии. Образуют восточную окраину впадины озера Копаис[3][1] и северную окраину озёр Илики и Паралимни. Простирается до залива Вориос-Эввоикос. Высочайшая вершина — Петалас (781 м). С древних времён известны храмом Аполлона Птойского[1][2], упомянутого Павсанием[4]. Руины храма находятся западнее действующего женского монастыря Пелагия, у вершины Птоон (724,1 м). В храме был оракул[5]. Раз в 4 года в Акрефии совершалось празднество «τὰ Πτώια» при храме Аполлона Птойского[6], включавшее музыкальные соревнования и юношеские состязания. Святилище расположено на трёх уровнях. На вершине находится храм, деревянный в архаический период, каменный храм в дорическом стиле построен в IV—III вв. до н. э. Перед храмом квадратная площадь с алтарями и жертвенниками. На среднем уровне расположены две стои. На нижнем уровне — большой бассейн конца IV века до н. э. В 1 км, в Кастраки (Καστράκι) находилось святилище местного героя и эпонима Птоя (Πτώος), датируемое IV веком до н. э. Псевдо-Аполлодор и Павсаний со ссылкой на поэта Асия Самосского сообщают, что эпоним Птой был сыном Афаманта и Фемисто[7][4]. Найдены статуи архаического периода, куросы (начало IV — начало V века до н. э.). С запада горы огибает автострада 1[1][2].

Птоон
греч. Πτώον
Высшая точка
Абсолютная высота	781[1][2] м
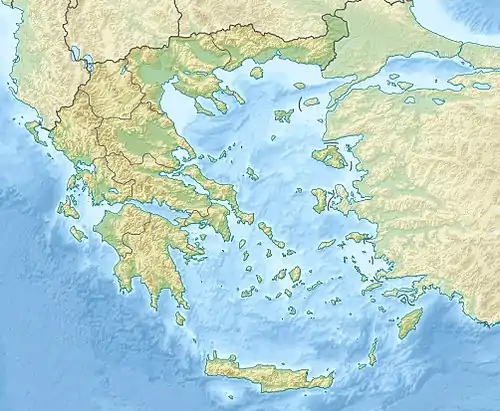
Расположение
38°28′52″ с. ш. 23°19′40″ в. д.
Страна	Греция
Периферия	Центральная Греция
Периферийная единица	Беотия
Птоон
Птоон
Медиафайлы на Викискладе