Поляриссима

Поляри́ссима (полярис от лат. polaris — полярный) — видимая звезда, предпочтительно яркая, находящаяся примерно на оси вращения Земли, то есть звезда, видимое положение которой близко к одному из полюсов мира, и которая находится в зените, если смотреть соответственно с северного или южного полюса Земли. Аналогичная концепция используется в отношении других планет.

Фотография полярной звезды и соседних звёзд (время экспозиции 45 мин).

В то время как видимое положение других звёзд на небе меняется в течение ночи, и кажется, что они вращаются вокруг небесного полюса, видимое положение поляриссим практически не меняется. Это делает поляриссимы особенно полезными в астрономической навигации: они являются надёжным указателем направления на соответствующие географические полюсы; их видимое положение на небе постоянно, благодаря чему их угол возвышения над горизонтом может быть использован для определения географической широты.

Поляриссимы Земли

На практике термином Полярис обычно называют Полярную звезду, которая является текущей поляриссимой северного полюса. Тогда как южный полюс в настоящее время лишён столь ярких звёзд, как Полярная, чтобы обозначить свою позицию. Ближайшая к этой точке видимая невооружённым глазом звезда — слабая Сигма Октанта, которую иногда называют Южной звездой.

С течением времени поляриссимами становятся разные звёзды. Это вызвано тем, что небесные полюса непрерывно дрейфуют через звёздное поле. Основная причина этого — прецессия оси вращения Земли. Если бы звёзды были неподвижными в пространстве, прецессия привела бы к тому, что небесные полюса совершали бы воображаемые круги на небесной сфере, делая один круг примерно за 26 000 лет и проходя вблизи различных звёзд в разные времена. Вдобавок сами звёзды движутся относительно друг друга, и это так называемое собственное движение звёзд является ещё одной причиной смены поляриссим.

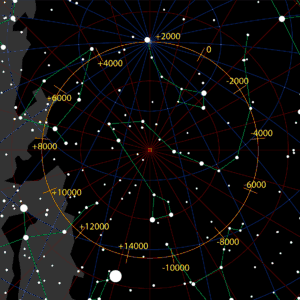
Прецессия земной оси вокруг северного полюса эклиптики и соответствующая смена полярных звёзд

Прецессия земной оси вокруг южного полюса эклиптики и соответствующая смена полярных звёзд

Список северных полярных звёзд полного прецессионного круга[1]

13 тыс. лет до н. э. — полярная звезда — Вега (α (альфа) Лиры)
9 тыс. лет до н. э. — полярные звезды (поочерёдно) π (пи) и η (эта) Геркулеса
8—7 тыс. лет до н. э. — полярная звезда — τ (тау) Геркулеса
5500—3500 гг. до н. э. — полярная звезда — Эдасих ι (йота) Дракона
3500—1500 гг. до н. э. — полярная звезда — Тубан α (альфа) Дракона)
1500 г. до н. э. — 1 год н. э. — полярная звезда — Кохаб (β (бета) Малой Медведицы).
1—1100 года — полярной звезды нет. Но есть «стражи» — Кохаб (β (бета) Малой Медведицы) и α (Альфа) Малой Медведицы, полюс примерно на одинаковом расстоянии от α и β Малой медведицы.
1100—3200 гг. Полярной звездой является α (альфа) Малой Медведицы. На минимальном расстоянии от северного полюса (0°27′34,1″) она пройдёт 23 апреля 2102 года.
3200—5000 гг. — полярной будет Альраи γ (гамма) Цефея.
5000—6500 гг. — полярная — Альфирк β (Бета) Цефея.
6500—8500 гг. — полярная — Альдерамин α (альфа) Цефея.
8500—13 000 гг. — полярные — Денеб α (альфа) и Садр γ (гамма) (Лебедя).
13 000 г. — полярной опять станет Вега (α (альфа) Лиры).

Другие планеты

Поляриссимы других планет определяются аналогично: это звёзды, которые наиболее близко совпадают с проекцией оси вращения планеты на небесной сфере. Различные планеты имеют разные поляриссимы, потому что их оси вращения ориентированы по-разному.

Планета / спутник	Южный полюс	Северный полюс
Меркурий	Альфа Живописца	Омикрон Дракона
Венера	ближайшая к южному полюсу Эта¹ Золотой рыбы	Фафнир
Луна	Дельта Золотой рыбы	Омикрон Дракона
Марс	Каппа Парусов (удалена на несколько градусов от южного полюса)	две звезды Северного креста — Садр и Денеб
Сатурн	Дельта Октанта
Уран	15 Ориона	Эта Змееносца[2]
Нептун	Гамма Парусов	посередине между Гаммой и Дельтой Лебедя

Примечания

Астрономия // Энциклопедия для детей. — М.: Аванта+, 2007. — С. 269.
Roger W. Sinnott. What defines a planet’s north pole? (неопр.). Sky & Telescope (21 июля 2006). Дата обращения: 27 января 2017.

Ссылки

Поляриссима // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
Leeuwen, F. HIP 11767 (неопр.). Hipparcos, the New Reduction (2007). Дата обращения: 1 марта 2011.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Аванта-1] Астрономия // Энциклопедия для детей. — М.: Аванта+, 2007. — С. 269.

[2] Roger W. Sinnott. What defines a planet’s north pole? (неопр.). Sky & Telescope (21 июля 2006). Дата обращения: 27 января 2017.