Модель Белла — Лападулы
Модель Белла — Лападулы — модель контроля и управления доступом, основанная на мандатной модели управления доступом. В модели анализируются условия, при которых невозможно создание информационных потоков от субъектов с более высоким уровнем доступа к субъектам с более низким уровнем доступа.
История
Классическая модель Белла — Лападулы была описана в 1975 году сотрудниками компании MITRE Corporation Дэвидом Беллом и Леонардом Лападулой, к созданию модели их подтолкнула система безопасности для работы с секретными документами Правительства США[1][2][3]. Суть системы заключалась в следующем: каждому субъекту (лицу, работающему с документами) и объекту (документам) присваивается метка конфиденциальности, начиная от самой высокой («особой важности»), заканчивая самой низкой («несекретный» или «общедоступный»). Причем субъект, которому разрешён доступ только к объектам с более низкой меткой конфиденциальности, не может получить доступ к объекту с более высокой меткой конфиденциальности. Также субъекту запрещается запись информации в объекты с более низким уровнем безопасности.
Особенности
Модель Белла — Лападулы является моделью разграничения доступа к защищаемой информации. Она описывается конечным автоматом с допустимым набором состояний, в которых может находиться информационная система. Все элементы, входящие в состав информационной системы, разделены на две категории — субъекты и объекты. Каждому субъекту присваивается свой уровень доступа, соответствующий степени конфиденциальности. Аналогично, объекту присваивается уровень секретности. Понятие защищённой системы определяется следующим образом: каждое состояние системы должно соответствовать политике безопасности, установленной для данной информационной системы. Переход между состояниями описывается функциями перехода.
Система находится в безопасном состоянии в том случае, если у каждого субъекта имеется доступ только к тем объектам, к которым разрешен доступ на основе текущей политики безопасности. Для определения, имеет ли субъект права на получение определенного вида доступа к объекту, уровень секретности субъекта сравнивается с уровнем секретности объекта, и на основе этого сравнения решается вопрос, предоставить или нет запрашиваемый доступ. Наборы уровень доступа/уровень секретности описываются с помощью матрицы доступа.
Основными правилами, обеспечивающими разграничение доступа, являются следующие:
Простое свойство безопасности (The Simple Security)
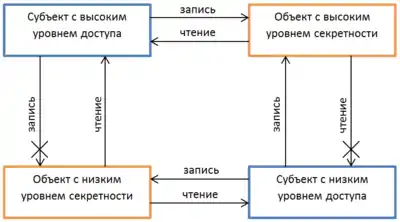
Субъект с уровнем доступа может читать информацию из объекта с уровнем секретности лишь тогда, когда преобладает над . Это правило также известно под названием «нет чтения верхнего» (NRU). Например, если субъект, имеющий доступ только к несекретным данным, попытается прочесть объект с уровнем секретности "совершенно секретно", то ему будет отказано в этом.
Свойство * (The *-property)
Субъект с уровнем секретности xs может писать информацию в объект с уровнем безопасности xо только если xо преобладает над . Это правило также известно под названием «нет записи вниз» (NWD). Например, если субъект, имеющий уровень доступа совершенно секретно, попытается записать в объект с уровнем секретности секретно, то ему будет отказано в этом.
Дискреционное свойство безопасности (The Discretionary Security Property)
Заключается в том, что права дискреционного доступа субъекта к объекту определяются на основе матрицы доступа.
Формальное описание модели
Обозначения
- — множество субъектов;
- — множество объектов, ;
- — множество прав доступа, — доступ на чтение, — доступ на запись;
- — множество уровней секретности, — Unclassified, — Sensitive but unclassified, C - Confidential, — Secret, — Top secret;
- — решётка уровней секретности, где:
- — множество состояний системы, представляемое в виде набора упорядоченных пар , где:
- — функция уровней секретности, ставящая в соответствие каждому объекту и субъекту в системе определённый уровень секретности;
- — матрица текущих прав доступа.
Оператор отношения обладает следующими свойствами:
- Рефлексивность: , данное свойство означает, что между субъектами и объектами одного уровня безопасности передача информации разрешена.
- Антисимметричность: , свойство означает, что если информация может передаваться от субъектов и объектов уровня A к субъектам и объектам уровня B, так и от субъектов и объектов уровня B к субъектам и объектам уровня A, то эти уровни эквивалентны.
- Транзитивность: , свойство означает, что если информации может передаваться от субъектов и объектов уровня A к субъектам и объектам уровня B, и от субъектов и объектов уровня B к субъектам и объектам уровня C, то она может передаваться от субъектов и объектов уровня A к субъектам и объектам уровня C.
Оператор наименьшей верхней границы определяется следующим отношением:
Оператор наибольшей нижней границы определяется следующим отношением:
Исходя из определения этих двух операторов можно показать, что для каждой пары существует единственный элемент наименьшей верхней границы и единственный элемент наибольшей нижней границы.
Система в модели Белла — Лападулы состоит из следующих элементов:
- — начальное состояние системы;
- — множество прав доступа;
- — функция перехода, которая в ходе выполнения запросов переводит систему из одного состояния в другое.
Определения состояния безопасности
Состояние называется достижимым в системе , если существует последовательность Начальное состояние является достижимым по определению.
Состояние системы называется безопасным по чтению (или simple-безопасным), если для каждого субъекта, осуществляющего в этом состоянии доступ по чтению к объекту, уровень безопасности субъекта доминирует над уровнем безопасности объекта:
Состояние системы называется безопасным по записи (или * — безопасным) в случае, если для каждого субъекта, осуществляющего в этом состоянии доступ по записи к объекту, уровень безопасности объекта доминирует над уровнем безопасности субъекта:
Состояние называется безопасным, если оно безопасно по чтению и по записи.
Система называется безопасной, если её начальное состояние безопасно, и все состояния, достижимые из путём применения конечной последовательности запросов из , безопасны.
Основная теорема безопасности Белла — Лападулы
Система безопасна тогда и только тогда, когда выполнены следующие условия:
- Начальное состояние безопасно.
- Для любого состояния , достижимого из путём применения конечной последовательности запросов из , таких, что и , для выполнены условия:
- Если и , то
- Если и , то
- Если и , то
- Если и , то
Докажем необходимость утверждения
Пусть система безопасна. В этом случае начальное состояние безопасно по определению. Предположим, что существует безопасное состояние , достижимое из состояния , и для данного перехода нарушено одно из условий 1-4. Легко заметить, что в случае, если нарушены условия 1 или 2, то состояние будет небезопасным по чтению, а если нарушены условия 3 или 4 – небезопасным по записи. В обоих случаях мы получаем противоречие с тем, что состояние является безопасным.
Докажем достаточность утверждения.
Система может быть небезопасной в двух случаях:
- В случае если начальное состояние небезопасно. Однако данное утверждение противоречит условию теоремы.
- Если существует небезопасное состояние , достижимое из безопасного состояния путём применения конечного числа запросов из . Это означает, что на каком-то промежуточном этапе произошёл переход , где – безопасное состояние, а - небезопасное. Однако условия 1-4 делают данный переход невозможным.
Недостатки
В силу своей простоты, классическая модель Белла — Лападулы имеет ряд серьёзных недостатков:
- Запрет записи «вниз». В модели Белла — Лападулы невозможна запись от объектов с более высоким уровнем конфиденциальности к объектам с более низким уровнем. Например, невозможно переписать сообщение класса top secret в класс secret, хотя иногда это бывает необходимо[4].
- Отсутствие многоуровневых объектов. Допускается чтение и запись информации между объектами только одного уровня. Например, при чтении информации уровня конфиденциальности unclassified из сообщения класса secret, система будет вынуждена присвоить читаемой информации класс secret[4].
- Отсутствие универсальности применения. Например, в военных системах передачи сообщений, должны определяться особые правила безопасности, которые отсутствуют в других приложениях модели. Такие правила не описаны моделью Белла — Лападулы, и поэтому должны быть определены вне модели[6]
- Как и для других моделей мандатного управления доступом, характерно наличие скрытых каналов передачи информации.
Удаленное чтение
В распределенной системе чтение инициируется запросом записи в объект с более низким уровнем секретности, что является нарушением правил классической модели Белла — Лападулы.
См. также
Примечания
- Bell, David Elliott and LaPadula, Leonard J. Secure Computer Systems: Mathematical Foundations (неопр.). — MITRE Corporation, 1973. Архивировано 18 июня 2006 года.
- Bell, David Elliott and LaPadula, Leonard J. Secure Computer System: Unified Exposition and Multics Interpretation (англ.) : journal. — MITRE Corporation, 1976.
- Bell, David Elliott (December 2005). «Looking Back at the Bell-LaPadula Model» (PDF). Proceedings of the 21st Annual Computer Security Applications Conference: 337–351. DOI:10.1109/CSAC.2005.37. Slides — Looking Back at the Bell-LaPadula Model Архивная копия от 8 июня 2008 на Wayback Machine
Литература
- Цирлов В. Л. Основы информационной безопасности автоматизированных систем. — Р.: Феникс, 2008. С. 40-44 ISBN 978-5-222-13164-0
- Девянин П. Н. Модели безопасности компьютерных систем: Учебное пособие для студентов высших учебных заведений. — М.: Издательский центр «Академия», 2005. С. 55-66 ISBN 5-7695-2053-1
- Грушо А. А., Тимонина Е. Е. Теоретические основы защиты информации. — М.: Издательство Агентства «Яхтсмен», 1996. С 52-55
- А. П. Баранов, Н. П. Борисенко, П. Д. Зегжда, А. Г. Ростовцев, Корт С. С. — Математические основы информационной безопасности. — М.: Издательство Агентства «Яхтсмен», 1997. C 22-36 https://web.archive.org/web/20110611052603/http://www.ssl.stu.neva.ru/sam/Book97.pdf