Математическая морфология

Структурный элемент представляет собой некоторое двоичное изображение (геометрическую форму). Он может быть произвольного размера и произвольной структуры. Чаще всего используются симметричные элементы, как прямоугольник фиксированного размера (BOX(l, w)), или круг некоторого диаметра (DISK (d)). В каждом элементе выделяется особая точка, называемая начальной (origin). Она может быть расположена в любом месте элемента (и вне его[1]), хотя в симметричных это обычно центральный пиксель.

Наиболее распространенные структурные элементы: BOX[H,W] -прямоугольник заданного размера, DISK[R] — диск заданного размера, RING[R] — кольцо заданного размера.

В начале результирующая поверхность заполняется 0, образуя полностью белое изображение. Затем осуществляется зондирование (probing) или сканирование исходного изображения пиксель за пикселем структурным элементом. Для зондирования каждого пикселя на изображение «накладывается» структурный элемент так, чтобы совместились зондируемая и начальные точки. Затем проверяется некоторое условие на соответствие пикселей структурного элемента и точек изображения «под ним». Если условие выполняется, то на результирующем изображении в соответствующем месте ставится 1 (в некоторых случаях будет добавляться не один единичный пиксель, а все единички из структурного элемента).

По рассмотренной выше схеме выполняются базовые операции. Такими операциями являются расширение и сужение. Производные операции — это некоторая комбинация базовых, выполняемых последовательно. Основными из них являются открытие и закрытие.

Пример переноса при t=(2,1).

Операция переноса X_t множества пикселов X на вектор t задаётся в виде X_t={x+t|x∈X}. Следовательно, перенос множества единичных пикселов на бинарном изображении сдвигает все пикселы множества на заданное расстояние. Вектор переноса t может задаваться в виде упорядоченной пары (∆r,∆c), где ∆r — компонент вектора переноса в направлении строк, а ∆c — компонент вектора переноса в направлении столбцов изображения.

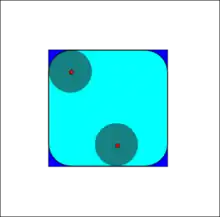
Наращивание бинарного изображения A структурным элементом B обозначается ${\displaystyle A\oplus B}$ и задаётся выражением:

${\displaystyle A\oplus B=\bigcup _{b\in B}A_{b}}$.

В данном выражении оператор объединения можно считать оператором, применяемым в окрестности пикселов. Структурный элемент B применяется ко всем пикселам бинарного изображения. Каждый раз, когда начало координат структурного элемента совмещается с единичным бинарным пикселом, ко всему структурному элементу применяется перенос и последующее логическое сложение (логическое ИЛИ) с соответствующими пикселами бинарного изображения. Результаты логического сложения записываются в выходное бинарное изображение, которое изначально инициализируется нулевыми значениями.

Наращивание темно синего квадрата дисковым структурным элементом, результирующего на ярко-голубой квадрат с закругленными концами.

Эрозия бинарного изображения А структурным элементом В обозначается ${\displaystyle A\ominus B}$ и задаётся выражением:

${\displaystyle A\ominus B=\{z\in A|B_{z}\subseteq A\}}$.

При выполнении операции эрозии структурный элемент тоже проходит по всем пикселам изображения. Если в некоторой позиции каждый единичный пиксел структурного элемента совпадет с единичным пикселом бинарного изображения, то выполняется логическое сложение центрального пиксела структурного элемента с соответствующим пикселом выходного изображения. В результате применения операции эрозии все объекты, меньшие чем структурный элемент, стираются, объекты, соединённые тонкими линиями становятся разъединёнными и размеры всех объектов уменьшаются.

Эрозия темно синего квадрата дисковым структурным элементом, результирующего на ярко-голубой квадрат.

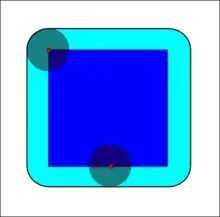
Замыкание темно синей формы (объединение двух квадратов) дисковым структурным элементом, результирующего на темно синюю форму и светло-голубые площади.

Замыкание бинарного изображения А структурным элементом В обозначается ${\displaystyle A\bullet B}$ и задаётся выражением:

${\displaystyle A\bullet B=(A\oplus B)\ominus B}$.

Операция замыкания «закрывает» небольшие внутренние «дырки» в изображении, и убирает углубления по краям области. Если к изображению применить сначала операцию наращивания, то мы сможем избавиться от малых дыр и щелей, но при этом произойдёт увеличение контура объекта. Избежать этого увеличения позволяет операция эрозия, выполненная сразу после наращивания с тем же структурным элементом.

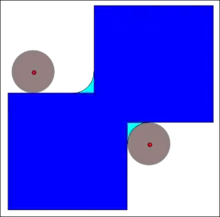
Размыкание темно-синего квадрата дисковым структурным элементом, результирующего на светло синий квадрат с закругленными углами.

Размыканием бинарного изображения А структурным элементом В обозначается ${\displaystyle A\circ B}$ и задаётся выражением:

${\displaystyle A\circ B=(A\ominus B)\oplus B}$.

Операция эрозии полезна для удаления малых объектов и различных шумов, но у этой операции есть недостаток — все остающиеся объекты уменьшаются в размере. Этого эффекта можно избежать, если после операции эрозии применить операцию наращивания с тем же структурным элементом. Размыкание отсеивает все объекты, меньшие чем структурный элемент, но при этом помогает избежать сильного уменьшения размера объектов. Также размыкание идеально подходит для удаления линий, толщина которых меньше, чем диаметр структурного элемента. Также важно помнить, что после этой операции контуры объектов становятся более гладкими.