Лемма Александрова
Лемма Александрова — утверждение нейтральной геометрии и сферической геометрии, играющее важную роль в основаниях александровской геометрии.
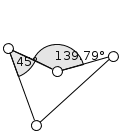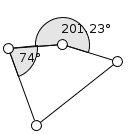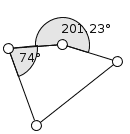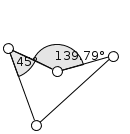
Монотонная зависимость углов друг от друга.
Формулировка
Зафиксируем вещественное число и обозначим через модельную плоскость кривизны . То есть
- есть евклидова плоскость,
- при есть сфера радиуса ,
- при есть плоскость Лобачевского кривизны .
Пусть и — два четырёхугольника в с равными соответствующими сторонами. Предположим, точки и лежат по разные стороны от прямой , точка лежит на кратчайшей . Тогда следующие выражения имеют один и тот же знак:
История
Лемма появляется в книге Александров, А. Д. Внутренняя геометрия выпуклых поверхностей. — Теортехиздат, 1948.
Литература
- Бураго Д.Ю., Бураго Ю.Д., Иванов С.В. Курс метрической геометрии. — 2004. — ISBN 5-93972-300-4.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.