Кинк (математика)

Вид ${\displaystyle V(\phi )}$ при ${\displaystyle \lambda =2,~~\mu ={\sqrt {2}}}$.

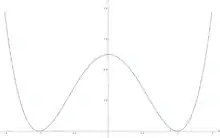
Рассмотрим[1] теорию одного действительного скалярного поля в пространстве размерности ${\displaystyle 1+1}$ с действием

${\displaystyle S=\int d^{2}x\left[{\frac {1}{2}}\phi _{,\mu }\phi ^{,\mu }-V(\phi )\right],}$

где ${\displaystyle \phi }$ — потенциал поля, ${\displaystyle \mu =0,1}$, а

${\displaystyle V(\phi )=-{\frac {\mu ^{2}}{2}}\phi ^{2}+{\frac {\lambda }{4}}\phi ^{4}+{\frac {\mu ^{2}}{4\lambda }}={\frac {\lambda }{4}}(\phi ^{2}-v^{2})^{2},~~v={\frac {\mu }{\sqrt {\lambda }}}.}$

Действие инвариантно относительно дискретного преобразования ${\displaystyle \phi =-\phi }$; эта симметрия спонтанно нарушается, так как классические вакуумы равны ${\displaystyle \phi ^{vac}=\pm v}$.

Из принципа наименьшего действия получается уравнение поля

${\displaystyle \phi _{,\mu }^{~~\mu }+{\frac {\partial V(\phi )}{\partial \phi }}=0.}$

Гиперболический тангенс — статическое решение уравнений поля при ${\displaystyle x_{0}=0,~~\lambda =2,~~\mu ={\sqrt {2}}}$.

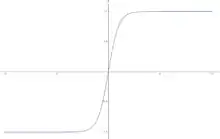
Будем искать статическое, то есть не зависящее от времени решение уравнений поля. В этом случае уравнение поля сводится к

${\displaystyle \phi ''-{\frac {\partial V(\phi )}{\partial \phi }}=0,}$

где штрих обозначает производную по пространственной координате. Полученное уравнение имеет следующее решение:

${\displaystyle \phi =v\tanh(\pm {\sqrt {\frac {\lambda }{2}}}v(x-x_{0}))={\frac {\mu }{\sqrt {\lambda }}}\tanh {(\pm {\frac {\mu }{\sqrt {2}}}x)},}$

где ${\displaystyle x_{0}}$ — постоянная интегрирования. Данное решение и является простейшим статическим кинком, интерполирующим между вакуумами ${\displaystyle -v}$ и ${\displaystyle +v}$ при изменении пространственной координаты от ${\displaystyle -\infty }$ до ${\displaystyle +\infty }$. Решение со знаком ${\displaystyle -}$ называется антикинком.

Рассмотрим[1] теорию одного комплексного скалярного поля в пространстве размерности ${\displaystyle 1+1}$ с лагранжианом

${\displaystyle \Lambda =\phi _{,\mu }{\bar {\phi }}^{,\mu }+\mu ^{2}\phi {\bar {\phi }}-{\frac {\lambda }{2}}(\phi {\bar {\phi }})^{2}.}$

Принцип наименьшего действия приводит к следующим уравнениям поля:

${\displaystyle \phi _{,\mu }^{~~\mu }=\mu ^{2}\phi -\lambda \phi ^{2}{\bar {\phi }},}$

${\displaystyle {\bar {\phi }}_{,\mu }^{,\mu }=\mu ^{2}{\bar {\phi }}-\lambda {\bar {\phi }}^{2}\phi .}$

Полученные уравнения имеют решением кинк из теории действительного скалярного поля

${\displaystyle \phi ={\bar {\phi }}={\frac {\mu }{\sqrt {\lambda }}}\tanh {(\pm {\frac {\mu }{\sqrt {2}}}x)}.}$

Кинк в уравнении синус-Гордона

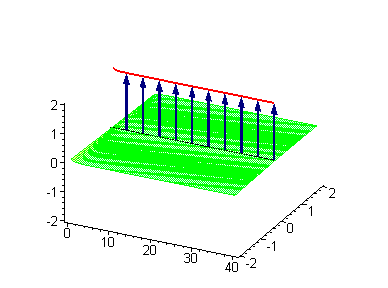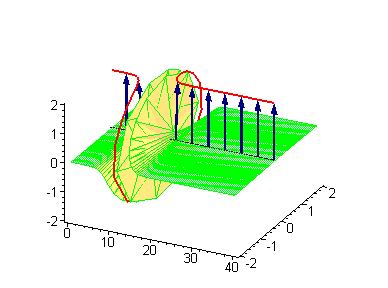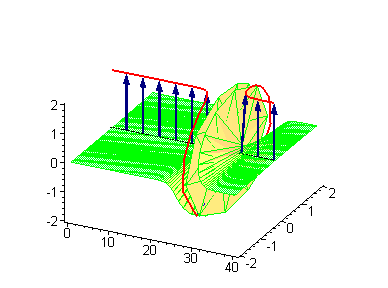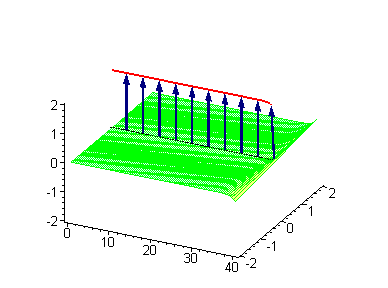
Рассмотрим[1] теорию одного действительного скалярного поля в пространстве размерности ${\displaystyle 1+1}$ с лагранжианом

${\displaystyle \Lambda =\phi _{,\mu }\phi ^{,\mu }+m^{2}v^{2}[\cos {\frac {\phi }{v}}-1].}$

Принцип наименьшего действия приводит к уравнению

${\displaystyle \phi _{,\mu }^{~~\mu }+m^{2}v\sin {\frac {\phi }{v}}=0,}$

Антикинк в уравнении синус-Гордона

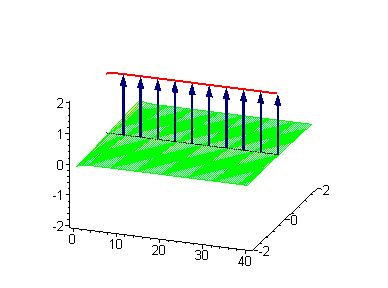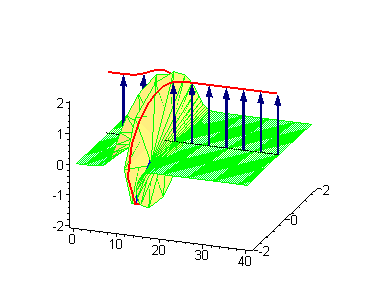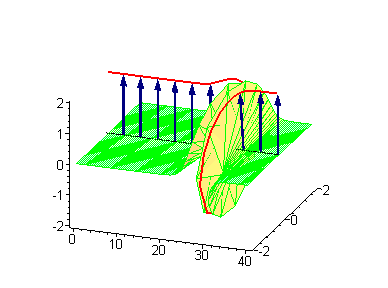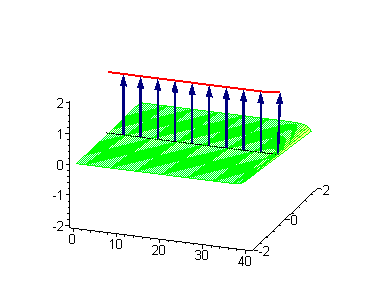
которое заменой ${\displaystyle x\rightarrow mx,~~t\rightarrow mt,~~\phi \rightarrow {\frac {\phi }{v}}}$ приводится к уравнению синус-Гордона

${\displaystyle \phi _{tt}-\phi _{xx}+\sin \phi =0,}$

имеющему следующие частные решения[2], представляющие движущиеся со скоростью ${\displaystyle v}$ кинки, интерполирующие между вакуумами ${\displaystyle \phi _{0}=2\pi k,~~k\in \mathbb {Z} }$ и ${\displaystyle \phi _{0}+2\pi }$ при изменении ${\displaystyle x}$ от ${\displaystyle -\infty }$ до ${\displaystyle +\infty }$:

${\displaystyle \phi (x,t)=\phi _{0}+4\arctan \left\{\exp \left[\pm {\frac {x+vt}{\sqrt {v^{2}-1}}}+\delta \right]\right\},}$

где ${\displaystyle \delta }$ — произвольная постоянная. Знак ${\displaystyle +}$ соответствует кинку, знак ${\displaystyle -}$ — антикинку.

• Т. И. Белова, А. Е. Кудрявцев, Солитоны и их взаимодействия в классической теории поля, УФН 167, 377—406 (1997).
• V.A. Gani, A.E. Kudryavtsev, M.A. Lizunova, Kink interactions in the (1+1)-dimensional φ⁶ model, Phys. Rev. D 89, 125009 (2014); arXiv:1402.5903 [hep-th].
• V.A. Gani, V. Lensky, M.A. Lizunova, Kink excitation spectra in the (1+1)-dimensional φ⁸ model, JHEP 08 (2015) 147; arXiv:1506.02313 [hep-th].