Ирисы Фишера

Ирисы Фишера — это набор данных для задачи классификации, на примере которого Рональд Фишер в 1936 году продемонстрировал работу разработанного им метода дискриминантного анализа.[1] Иногда его также называют ирисами Андерсона, так как данные были собраны американским ботаником Эдгаром Андерсоном.[2] Этот набор данных стал уже классическим, и часто используется в литературе для иллюстрации работы различных статистических алгоритмов.[3]

Диаграмма рассеяния ирисов Фишера

Описание

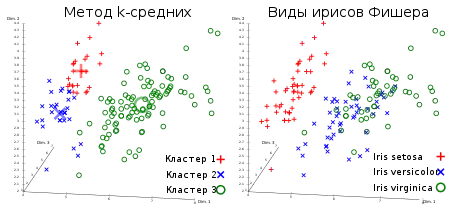
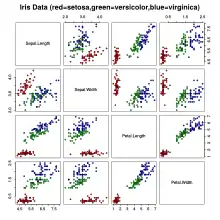
Ирисы Фишера состоят из данных о 150 экземплярах ириса, по 50 экземпляров из трёх видов — Ирис щетинистый (Iris setosa), Ирис виргинский (Iris virginica) и Ирис разноцветный (Iris versicolor). Для каждого экземпляра измерялись четыре характеристики (в сантиметрах):

Длина наружной доли околоцветника (англ. sepal length);
Ширина наружной доли околоцветника (англ. sepal width);
Длина внутренней доли околоцветника (англ. petal length);
Ширина внутренней доли околоцветника (англ. petal width).

На основании этого набора данных требуется построить правило классификации, определяющее вид растения по данным измерений. Это задача многоклассовой классификации, так как имеется три класса — три вида ириса.

Один из классов (Iris setosa) линейно-разделим от двух остальных.

Набор данных

Ирисы Фишера

Длина чашелистика	Ширина чашелистика	Длина лепестка	Ширина лепестка	Вид ириса
5.1	3.5	1.4	0.2	setosa
4.9	3.0	1.4	0.2	setosa
4.7	3.2	1.3	0.2	setosa
4.6	3.1	1.5	0.2	setosa
5.0	3.6	1.4	0.2	setosa
5.4	3.9	1.7	0.4	setosa
4.6	3.4	1.4	0.3	setosa
5.0	3.4	1.5	0.2	setosa
4.4	2.9	1.4	0.2	setosa
4.9	3.1	1.5	0.1	setosa
5.4	3.7	1.5	0.2	setosa
4.8	3.4	1.6	0.2	setosa
4.8	3.0	1.4	0.1	setosa
4.3	3.0	1.1	0.1	setosa
5.8	4.0	1.2	0.2	setosa
5.7	4.4	1.5	0.4	setosa
5.4	3.9	1.3	0.4	setosa
5.1	3.5	1.4	0.3	setosa
5.7	3.8	1.7	0.3	setosa
5.1	3.8	1.5	0.3	setosa
5.4	3.4	1.7	0.2	setosa
5.1	3.7	1.5	0.4	setosa
4.6	3.6	1.0	0.2	setosa
5.1	3.3	1.7	0.5	setosa
4.8	3.4	1.9	0.2	setosa
5.0	3.0	1.6	0.2	setosa
5.0	3.4	1.6	0.4	setosa
5.2	3.5	1.5	0.2	setosa
5.2	3.4	1.4	0.2	setosa
4.7	3.2	1.6	0.2	setosa
4.8	3.1	1.6	0.2	setosa
5.4	3.4	1.5	0.4	setosa
5.2	4.1	1.5	0.1	setosa
5.5	4.2	1.4	0.2	setosa
4.9	3.1	1.5	0.2	setosa
5.0	3.2	1.2	0.2	setosa
5.5	3.5	1.3	0.2	setosa
4.9	3.6	1.4	0.1	setosa
4.4	3.0	1.3	0.2	setosa
5.1	3.4	1.5	0.2	setosa
5.0	3.5	1.3	0.3	setosa
4.5	2.3	1.3	0.3	setosa
4.4	3.2	1.3	0.2	setosa
5.0	3.5	1.6	0.6	setosa
5.1	3.8	1.9	0.4	setosa
4.8	3.0	1.4	0.3	setosa
5.1	3.8	1.6	0.2	setosa
4.6	3.2	1.4	0.2	setosa
5.3	3.7	1.5	0.2	setosa
5.0	3.3	1.4	0.2	setosa
7.0	3.2	4.7	1.4	versicolor
6.4	3.2	4.5	1.5	versicolor
6.9	3.1	4.9	1.5	versicolor
5.5	2.3	4.0	1.3	versicolor
6.5	2.8	4.6	1.5	versicolor
5.7	2.8	4.5	1.3	versicolor
6.3	3.3	4.7	1.6	versicolor
4.9	2.4	3.3	1.0	versicolor
6.6	2.9	4.6	1.3	versicolor
5.2	2.7	3.9	1.4	versicolor
5.0	2.0	3.5	1.0	versicolor
5.9	3.0	4.2	1.5	versicolor
6.0	2.2	4.0	1.0	versicolor
6.1	2.9	4.7	1.4	versicolor
5.6	2.9	3.6	1.3	versicolor
6.7	3.1	4.4	1.4	versicolor
5.6	3.0	4.5	1.5	versicolor
5.8	2.7	4.1	1.0	versicolor
6.2	2.2	4.5	1.5	versicolor
5.6	2.5	3.9	1.1	versicolor
5.9	3.2	4.8	1.8	versicolor
6.1	2.8	4.0	1.3	versicolor
6.3	2.5	4.9	1.5	versicolor
6.1	2.8	4.7	1.2	versicolor
6.4	2.9	4.3	1.3	versicolor
6.6	3.0	4.4	1.4	versicolor
6.8	2.8	4.8	1.4	versicolor
6.7	3.0	5.0	1.7	versicolor
6.0	2.9	4.5	1.5	versicolor
5.7	2.6	3.5	1.0	versicolor
5.5	2.4	3.8	1.1	versicolor
5.5	2.4	3.7	1.0	versicolor
5.8	2.7	3.9	1.2	versicolor
6.0	2.7	5.1	1.6	versicolor
5.4	3.0	4.5	1.5	versicolor
6.0	3.4	4.5	1.6	versicolor
6.7	3.1	4.7	1.5	versicolor
6.3	2.3	4.4	1.3	versicolor
5.6	3.0	4.1	1.3	versicolor
5.5	2.5	4.0	1.3	versicolor
5.5	2.6	4.4	1.2	versicolor
6.1	3.0	4.6	1.4	versicolor
5.8	2.6	4.0	1.2	versicolor
5.0	2.3	3.3	1.0	versicolor
5.6	2.7	4.2	1.3	versicolor
5.7	3.0	4.2	1.2	versicolor
5.7	2.9	4.2	1.3	versicolor
6.2	2.9	4.3	1.3	versicolor
5.1	2.5	3.0	1.1	versicolor
5.7	2.8	4.1	1.3	versicolor
6.3	3.3	6.0	2.5	virginica
5.8	2.7	5.1	1.9	virginica
7.1	3.0	5.9	2.1	virginica
6.3	2.9	5.6	1.8	virginica
6.5	3.0	5.8	2.2	virginica
7.6	3.0	6.6	2.1	virginica
4.9	2.5	4.5	1.7	virginica
7.3	2.9	6.3	1.8	virginica
6.7	2.5	5.8	1.8	virginica
7.2	3.6	6.1	2.5	virginica
6.5	3.2	5.1	2.0	virginica
6.4	2.7	5.3	1.9	virginica
6.8	3.0	5.5	2.1	virginica
5.7	2.5	5.0	2.0	virginica
5.8	2.8	5.1	2.4	virginica
6.4	3.2	5.3	2.3	virginica
6.5	3.0	5.5	1.8	virginica
7.7	3.8	6.7	2.2	virginica
7.7	2.6	6.9	2.3	virginica
6.0	2.2	5.0	1.5	virginica
6.9	3.2	5.7	2.3	virginica
5.6	2.8	4.9	2.0	virginica
7.7	2.8	6.7	2.0	virginica
6.3	2.7	4.9	1.8	virginica
6.7	3.3	5.7	2.1	virginica
7.2	3.2	6.0	1.8	virginica
6.2	2.8	4.8	1.8	virginica
6.1	3.0	4.9	1.8	virginica
6.4	2.8	5.6	2.1	virginica
7.2	3.0	5.8	1.6	virginica
7.4	2.8	6.1	1.9	virginica
7.9	3.8	6.4	2.0	virginica
6.4	2.8	5.6	2.2	virginica
6.3	2.8	5.1	1.5	virginica
6.1	2.6	5.6	1.4	virginica
7.7	3.0	6.1	2.3	virginica
6.3	3.4	5.6	2.4	virginica
6.4	3.1	5.5	1.8	virginica
6.0	3.0	4.8	1.8	virginica
6.9	3.1	5.4	2.1	virginica
6.7	3.1	5.6	2.4	virginica
6.9	3.1	5.1	2.3	virginica
5.8	2.7	5.1	1.9	virginica
6.8	3.2	5.9	2.3	virginica
6.7	3.3	5.7	2.5	virginica
6.7	3.0	5.2	2.3	virginica
6.3	2.5	5.0	1.9	virginica
6.5	3.0	5.2	2.0	virginica
6.2	3.4	5.4	2.3	virginica
5.9	3.0	5.1	1.8	virginica

Результат кластеризации методом k-средних для ирисов Фишера и реальные виды ирисов, визуализированные с помощью ELKI. Центры кластеров отмечены с помощью крупных, полупрозрачных маркеров.

Iris setosa

Iris virginica

Iris versicolor

Примечания

Fisher, R.A. The Use of Multiple Measurements in Taxonomic Problems (англ.) // Annals of Eugenics : journal. — 1936. — Vol. 7. — P. 179—188.
Edgar Anderson. The irises of the Gaspé Peninsula (неопр.) // Bulletin of the American Iris Society. — 1935. — Т. 59. — С. 2—5.
UCI Machine Learning Repository: Iris Data Set

Ссылки

«Ирисы Фишера» в UCI Machine Learning Repository (англ.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[fisher36-1] Fisher, R.A. The Use of Multiple Measurements in Taxonomic Problems (англ.) // Annals of Eugenics : journal. — 1936. — Vol. 7. — P. 179—188.

[anderson35-2] Edgar Anderson. The irises of the Gaspé Peninsula (неопр.) // Bulletin of the American Iris Society. — 1935. — Т. 59. — С. 2—5.

[uci-3] UCI Machine Learning Repository: Iris Data Set