Инверсный конгруэнтный метод
Инверсный конгруэнтный метод (или генератор Эйхенауэра — Лена, также возможно Эйченауэра — Лехна) — метод генерации псевдослучайных чисел, основанный на использовании обратного по модулю числа для генерации следующего члена последовательности.
Описание
Инверсный конгруэнтный метод был предложен Эйченауэром и Лехном в 1986 году[1] как замена линейному конгруэнтному методу, не обладающему решётчатой структурой[2].
Данный метод состоит в вычислении последовательности случайных чисел в кольце вычетов по модулю натурального числа .
Основным отличием от линейного метода является использование при генерации последовательности числа, обратного к предыдущему элементу, вместо самого предыдущего элемента.
Параметрами генератора являются[3]:
| — соль | |
| — множитель | |
| — приращение |
В случае простого n
Значение членов последовательности задается в виде:
if if
В случае составного n
Если число является составным, элементы последовательности вычисляются следующим образом:
Параметры подбираются таким образом, чтобы .
Период
Последовательность периодична, причём период не превышает размерности кольца . Максимальный период достигается в случае, если многочлен является примитивным. Достаточным условием максимального периода последовательности является такой выбор констант и , чтобы многочлен был неприводим[4].
В случае составного максимально возможный период равен (функция Эйлера)[5].
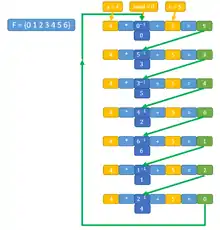
Пример
Инверсный конгруэнтный генератор с параметрами генерирует последовательность в кольце , где числа и , а также и обратны друг другу. В данном примере многочлен неприводим в и числа не являются его корнями, благодаря чему период максимален и равен .
Примеры реализации
Python
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = egcd(b % a, a)
return (g, x - (b // a) * y, y)
def modinv(a, m):
gcd, x, y = egcd(a, m)
if gcd != 1:
return None # modular inverse does not exist
else:
return x % m
def ICG(n, a, c, seed):
if (seed == 0):
return c
return (a * modinv(seed, n) + c) % n
seed = 1
n = 5
a = 2
c = 3
count = 10
for i in range(count):
print(seed)
seed = ICG(n, a, c, seed)
C++
#include <iostream>
using namespace std;
int mod_inv(int a, int n)
{
int b0 = n, t, q;
int x0 = 0, x1 = 1;
if (n == 1) return 1;
while (a > 1)
{
q = a / n;
t = n, n = a % n, a = t;
t = x0, x0 = x1 - q * x0, x1 = t;
}
if (x1 < 0) x1 += b0;
return x1;
}
int ICG(int n, int a, int c, int seed)
{
if (seed == 0)
return c;
return (a * mod_inv(seed, n) + c) % n;
}
int main(void)
{
int seed = 1;
int n = 5;
int a = 2;
int c = 3;
int count = 10;
for (int i = 0; i < count; i++)
{
cout << seed << endl;
seed = ICG(n, a, c, seed);
}
return 0;
}
Составные инверсные генераторы
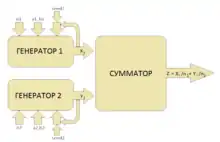
Основным недостатком инверсных конгруэнтных генераторов является возрастание сложности вычислений при увеличении периода. Данный недостаток исправлен в составных инверсных конгруэнтных генераторах.
Конструкция составных инверсных генераторов представляет из себя объединение двух или более инверсных конгруэнтных генераторов.
Пусть — различные простые числа, каждое . Для каждого индекса в пределах пусть — последовательность элементов с периодом . Другими словами, .
Пусть — последовательность случайных чисел в пределах , где .
Результирующая последовательность определяется как сумма: .
Период результирующей последовательности [6].
Одни из преимуществ данного подхода является возможность использовать инверсные конгруэнтные генераторы работающие параллельно.
Пример составного инверсного генератора
Пусть и . Для упрощения положим and . Для каждого вычислим .
Тогда . То есть мы получили последовательность с периодом .
Чтобы избавится от дробных чисел, мы может умножить каждый элемент полученной последовательности на и получить последовательность целых чисел:
Преимущества инверсных конгруэнтных генераторов
Инверсные конгруэнтные генераторы применяются в практических целях по ряду причин.
Во-первых, инверсные конгруэнтные генераторы обладают достаточно неплохой равномерностью[7], кроме того полученные последовательности совершенно лишены решетчатой структуры, характерной для линейных конгруэнтных генераторов[1][8][9].
Во-вторых, двоичные последовательности, полученные с помощью ИКГ не имеют нежелательных статистических отклонений. Полученные данным методом последовательности проверены рядом статистических тестов и остаются стабильными при изменении параметров[7][8][10][11].
В-третьих, составные генераторы обладают теми же свойствами, что и одиночные линейные инверсные генераторы[12], но при этом имеют период значительно превышающий период одиночных генераторов[13]. Кроме того, устройство составных генераторов позволяет добиться высокого прироста производительности при использовании на многопроцессорных системах[14].
Существует алгоритм, позволяющий разрабатывать составные генераторы, обладающие предсказуемыми длиной периода и уровнем сложности, а также хорошими статистическими свойствами выходных последовательностей [15].
Недостатки инверсных конгруэнтных генераторов
Основным недостатком инверсных конгруэнтных генераторов является медленная скорость генерации элементов последовательности: на вычисление одного элемента последовательности затрачивается операций умножения[16].
Примечания
- Кнут, 2013, с. 45.
- Eichenauer, Lehn, 1986.
- Hellekalek, 1995, p. 255: «We have to choose the modulus p, a multiplier a, an additive term b».
- Amy Glen: On the Period Length of Pseudorandom Number Sequences, 2002, 5.3, p. 67: «If x2-bx-a is a primitive polynomial over Fp then Xi has full period length p».
- Amy Glen: On the Period Length of Pseudorandom Number Sequences, 2002, 5.4, p. 69: «The sequence Xi is purely periodic with period length d ≤ φ(m)».
- Hellekalek, 1995, p. 256: «It is elementary to see that the period of the sequence (Xn)n equals M := p1*p2*...* pr».
- Eichenauer-Herrmannn, Niederreiter, 1992.
- Eichenauer-Herrmannn, 1991.
- Eichenauer-Herrmannn, Grothe, Niederreiter et al, 1990, p. 81: «These generators do not show the simple lattice structure of the widely used linear congruential generators».
- Eichenauer-Herrmannn, 1993.
- Hellekalek, 1995, p. 261: «The excellent theoretical and empirical properties of inversive methods remain stable under the variation of parameters, provided we have maximal period length».
- Bubicz, Stoklosa, 2006, p. 2: «Compound approach gives the same outstanding properties of produced sequences as single inversive generators».
- Bubicz, Stoklosa, 2006, p. 2: «Compound inversive generators allow obtaining period length significantly greater than obtained by a single ICG».
- Bubicz, Stoklosa, 2006, p. 2: «They seem to be designed for application with multiprocessor parallel hardware platforms».
- Bubicz, Stoklosa, 2006, p. 2: «There exists steady and simple way of parameter choice, based on the Chou algorithm. It guarantees maximum period length».
- Anne Gille-Genest: Pseudo-Random Numbers Generators, 2012, p. 12: «The main disadvantage of those both inverse generators is that a calculation of one random number takes O(log m) multiplication in Fm so the algorithm is not fast».
Литература
- Книги
- Кнут Д. Э. Искусство программирования: Том 2. Получисленные алгоритмы — 3 — М.: Вильямс, 2013. — 828 с. — ISBN 978-5-8459-0081-4
- Статьи
- Eichenauer J., Lehn J. A non-linear congruential pseudo random number generator (англ.) // Statistische Hefte — Springer Berlin Heidelberg, Springer Science+Business Media, 1986. — Vol. 27, Iss. 1. — P. 315—326. — ISSN 0932-5026; 1613-9798 — doi:10.1007/BF02932576
- Eichenauer-Herrmann J., Grothe H., Niederreiter H., Topuzoǧlu A. On the lattice structure of a nonlinear generator with modulus 2ᵅ (англ.) // J. Comput. Appl. Math. — Elsevier BV, 1990. — Vol. 31, Iss. 1. — P. 81—85. — ISSN 0377-0427; 1879-1778 — doi:10.1016/0377-0427(90)90338-Z
- Eichenauer-Herrmann J. Inversive congruential pseudorandom numbers avoid the planes (англ.) // Math. Comp. — AMS, 1991. — Vol. 56, Iss. 193. — P. 297—301. — ISSN 0025-5718; 1088-6842 — doi:10.2307/2008543
- Eichenauer-Herrmann J., Niederreiter H. Lower bounds for the discrepancy of inversive congruential pseudorandom numbers with power of two modulus (англ.) // Math. Comp. — AMS, 1992. — Vol. 58, Iss. 198. — P. 775—779. — ISSN 0025-5718; 1088-6842 — doi:10.2307/2153216
- Eichenauer-Herrmann J. Statistical independence of a new class of inversive congruential pseudorandom numbers (англ.) // Math. Comp. — AMS, 1993. — Vol. 60. — P. 375—384. — ISSN 0025-5718; 1088-6842 — doi:10.1090/S0025-5718-1993-1159168-9
- Chou W. S. On inversive maximal period polynomials over finite fields (англ.) // Appl. Algebr. Eng. Comm. — Springer Science+Business Media, 1995. — Vol. 6, Iss. 4. — P. 245—250. — ISSN 0938-1279; 1432-0622 — doi:10.1007/BF01235718
- Hellekalek P. Inversive pseudorandom number generators: concepts, results and links (англ.) // WSC'95: Proceedings, 1995 Winter Simulation Conference / D. Goldsman, C. Alexopoulos — Washington: IEEE Computer Society, 1995. — P. 255—262. — 1463 p. — ISBN 978-0-7803-3018-4 — doi:10.1145/224401.224612
- Bubicz J., Stoklosa J. Compound Inversive Congruential Generator Design Algorithm (англ.) // IMCSIT 2006: Proceedings of the 4th International Multiconference on Computer Science and Information Technology — Amman: ASPU, 2006. — Vol. 1. — P. 1—6.
- Gille-Genest Anne. Pseudo-Random Numbers Generators. — 2012. (недоступная ссылка)
- Glen Amy. On the Period Length of Pseudorandom Number Sequences // The University of Adelaide: Honours in Pure Mathematics. — 2002.