Изокоста

На экономических графиках линия изокосты отображает набор совокупностей экономических ресурсов, которые фирма может приобрести с учётом рыночных цен на ресурсы и при полном использовании своего бюджета.[1][2] Несмотря на схожесть с бюджетной прямой в теории потребления, линия изокосты используется прежде всего для максимально возможных уменьшения затрат в производстве и увеличения полезности. Так, уравнение линии изокосты для труда и капитала как двух факторов производства с фиксированной ценой выглядит следующим образом:

${\displaystyle rK+wL=C}$,

Прямые ${\displaystyle TC}$ представляют собой изокосты (прямые, отражающие определённый уровень общих затрат). ${\displaystyle Q}$ — изокванты. ${\displaystyle P_{L}}$ — стоимость единицы труда (${\displaystyle w}$ в тексте), а ${\displaystyle P_{K}}$ — стоимость единицы капитала (${\displaystyle r}$ в тексте).

где: ${\displaystyle w}$ означает размер оплаты труда, ${\displaystyle r}$ — арендную ставку капитала, ${\displaystyle K}$ — размер используемой суммы капитала, ${\displaystyle L}$ — объём трудозатрат, а ${\displaystyle C}$ — цена приобретения количества этих двух факторов.

Абсолютная величина наклона изокосты, в целях отображения которой капитал на схемах ассоциирован с вертикальной стороной графика, а труд — с горизонтальной, равна отношению удельных затрат труда и капитала:

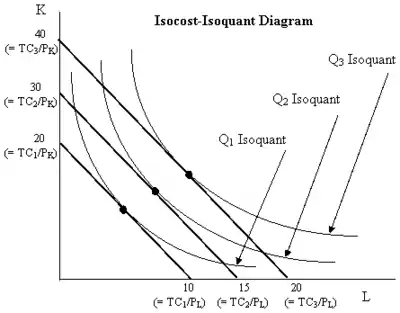
Линия изокосты изображается вместе с линией изокванты для определения наиболее приемлемой точки производства при том или ином количестве факторов. Точка касания между любой изоквантой и изокостой показывает наиболее дешёвую комбинацию факторов, которые способны произвести количество продукции, соответствующее данной изокванте. То есть, она показывает наибольший возможный уровень выпуска продукции при данном количестве факторов производства. Линия, соединяющая точки касания изокванты и изокосты (включая неизменные входные цены) — «путь расширения».[3]