Законы Осипова — Ланчестера
Законы Ланчестера (законы Осипова — Ланчестера) — математическая формула для расчета относительных сил пары сражающихся сторон — подразделений вооруженных сил. В статье «Влияние численности сражающихся сторон на их потери», опубликованной журналом «Военный сборник» в 1915 году, генерал-майор Корпуса военных топографов М. П. Осипов[1][2] описал математическую модель глобального вооружённого противостояния, практически применяемую в военном деле при описании убыли сражающихся сторон с течением времени и, входящую в математическую теорию исследования операций, на год опередив английского математика Ф. У. Ланчестера. Мировая война, две революции в России не позволили новой власти заявить в установленном в научной среде порядке об открытии царского офицера.
Уравнения Ланчестера — это дифференциальные уравнения, описывающие зависимость между силами сражающихся сторон A и D как функцию от времени, причем функция зависит только от A и D.[3]
В 1916 году, в разгар первой мировой войны, Фредерик Ланчестер разработал систему дифференциальных уравнений для демонстрации соотношения между противостоящими силами. Среди них есть так называемые Линейные законы Ланчестера (первого рода или честного боя, для рукопашного боя или неприцельного огня) и Квадратичные законы Ланчестера (для войн начиная с XX века с применением прицельного огня, дальнобойных орудий, огнестрельного оружия). В связи с установленным приоритетом в англоязычной литературе наметилась тенденция перехода от фразы «модель Ланчестера» к «модели Осипова — Ланчестера».[4].
Линейный закон Ланчестера
В древней битве, например между фалангами воинов, вооруженных копьями, один человек может бороться одновременно только с одним человеком. Если каждый человек убивает ровно одного (или погибает от одного) противника, то ожидаемое число воинов, оставшихся в конце сражения, — это просто разница между численностью большей и меньшей армий (при идентичности применяемого оружия).
Линейный закон применяется также к неприцельному огню по территории противника. Коэффициент убыли зависит от плотности имеющихся целей в целевой области, а также от количества стреляющих орудий. Если две группировки, занимающие одинаковую площадь и использующие одинаковые орудия, ведут огонь случайным образом по площадной цели одинакового размера, они будут убывать одинаковыми темпами до тех пор, пока меньшая группировка в конце концов не будет ликвидирована: большая вероятность поражения одним выстрелом какой-либо единицы крупной группировки уравновешивается большим числом выстрелов направленных на мелкую группировку.
Закон «честного боя»
- — первоначальное число единиц стороны A
- — численность войск, остающихся в армии A в момент времени
- — первоначальное число единиц стороны B
- — численность войск, остающихся в армии B в момент времени
- — Качество оружия ( 'E'xchange Rate) = (поражающая способность оружия стороны B) ÷ (поражающая способность оружия стороны A)
- (Истребительная сила) = (качество оружия) × (количество единиц)
Квадратичный закон Ланчестера
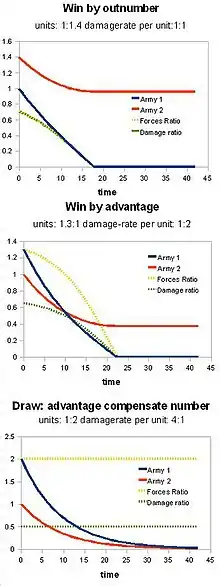
В современных боевых действиях, когда боевые единицы сторон удалены друг от друга и ведут прицельный огонь, они способны поражать несколько целей, и могут поражаться с нескольких направлений.
Коэффициент убыли (rate of attrition) зависит теперь только от количества боевых единиц, ведущих огонь. Ланчестер установил, что мощность группировки в этом случае пропорциональна не количеству боевых единиц, которое она имеет, а квадрату от числа единиц. Это называется квадратичным законом Ланчестера. Точнее, закон определяет потери боевых единиц, которые сражающаяся сторона нанесет за определенный период времени, по сравнению с теми, которые нанесет противостоящая сторона.
В своей базовой формулировке, этот закон полезен только для прогнозирования результатов и потерь за счет естественной убыли. Он не распространяется на целые армии, где тактическое развертывание предполагает, что не все боевые единицы будут задействованы всё время. Он работает, только когда каждый человек (или корабль, подразделение или иная боевая единица) может одновременно уничтожить только одного эквивалентного противника (поэтому он не применим к пулеметам, артиллерии, и к ядерному оружию).
Закон работает в предположении, что потери нарастают с течением времени: он не работает в ситуациях, в которых противостоящие войска убивают друг друга мгновенно, либо за счет одновременной стрельбы, либо если одна сторона выбывает с первого выстрела, получив большой урон. Заметим, что Квадратичный закон Ланчестера не относится к технологической силе, а только к численной силе, поэтому он предполагает N-квадрат-кратное увеличение качества для N-кратного увеличения количества.
Закон концентрации
- (Истребительная сила) = (качество оружия) × (количество единиц)
Примечания
- М. П. Осипов: к идентификации личности автора первой модели глобальных процессов
- Сергеев С. В., Долгов Е. И.. Осипов Михаил Павлович // Военные топографы Русской армии. — Москва: ЗАО «СиДи-Пресс», 2001.
- Lanchester Equations and Scoring Systems
- Митюков Н. В. «М. П. Осипов: К Идентификации личности автора первой модели глобальных процессов».. «Историческая психология и социология истории", № 2.. WebCite (2011 год.). Архивировано 15 августа 2013 года.
Части этой статьи скопированы с разрешения из статьи Эрнеста Адамса, опубликованной на веб-сайте разработчиков компьютерных игр Gamasutra. См. ссылки ниже.
Англоязычные ссылки
- «Kicking Butt By the Numbers: Закон Ланчестера», колонка Designer’s Notebook Эрнеста Адамса в веб-журнале Game Developer
- Уравнения и системы ранжирования Ланчестера, добавление к «Консолидация, рассредоточение и правило 3:1 в наземном сражении» Павла К. Дэвис, Рэнд корпорейшн публикации MR-638-AF/A/OSD
- Моделирование противостоящих сторон
Литература
- Вентцель Е. С., Лихтерев Я. М., Мильграм Ю. Г., Худяков И. В. Основы теории боевой эффективности и исследования операций. М.: ВВИА, 1961. 524 с.
- Helmbold, R. L. 1993. Osipov: The ‘Russian Lanchester’. European Journal of Operations Research 65: 278—288.
- Kipp, J. W. 2004. Tracking down Russia’s Lanchester. Journal of SlavicMilitary Studies 17: 257—269.
- Osipov, M. 1995. The Influence of the Numerical Strength of Engaged Forces in Their Casualties / transl. by R. L. Helmbold, A. S. Rehm. Naval Research Logistics 42: 435—490.
- Зенкин В.И. Курс математического и компьютерного моделирования.