Задача о 18 точках
Задача о 18 точках (парадокс 18 точек) — одна из задач вычислительной геометрии.
Формулировка
Поместим на отрезок точку с номером 1. Затем добавим ещё одну с номером 2 таким образом, чтобы они оказались в разных половинах отрезка. Третью точку добавим таким образом, чтобы все три находились в разных третях отрезка. Далее, для точки с номером должно выполняться условие, что все точки от первой до -й находились в различных частях отрезка длиной не более его общей длины.
Для каких можно построить такую последовательность ?
Ответ
Может показаться, что каждого целого должна существовать такая последовательность вещественных чисел . То есть такая, что для каждого целого и каждого целого найдётся такое , что выполняется неравенство
- ,
Однако, доказано[1], что таким образом можно поместить на отрезок максимум 17 точек, причём число различных порядков ограничено и равно 768[2].
Одно из 768 возможных решений:
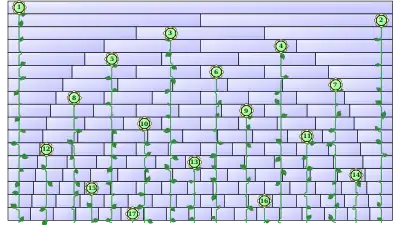
| 0.029 | |
| 0.971 | |
| 0.423 | |
| 0.71 | |
| 0.27 | |
| 0.542 | |
| 0.852 | |
| 0.172 | |
| 0.62 | |
| 0.355 | |
| 0.777 | |
| 0.1 | |
| 0.485 | |
| 0.905 | |
| 0.218 | |
| 0.667 | |
| 0.324 |
Примечания
- Berlekamp, E. R. и Graham, R. L. Irregularities in the Distributions of Finite Sequences. — 1970. — С. 152-161.
- Warmus, M. A Supplementary Note on the Irregularities of Distributions. — 1976. — С. 260-263.
Ссылки
- Weisstein, Eric W. 18-Point Problem (англ.) на сайте Wolfram MathWorld.