Задача Обервольфаха

На конференциях, проводимых в Обервольфахе, принято обедать вместе в зале с круглыми столами, не все из которых имеют один и тот же размер, а места за столами меняются от обеда к обеду. Задача Обервольфаха спрашивает, как задать распределение мест за столами, чтобы все места были заняты и все пары участников конференции сидели рядом только раз. Экземпляр задачи можно обозначить как ${\displaystyle OP(x,y,z,\dots )}$, где ${\displaystyle x,y,z,\dots }$ задаёт размеры столов. Альтернативно, когда некоторые размеры столов повторяются, это может отражаться как верхний индекс, например ${\displaystyle OP(5^{3})}$ описывает задачу с тремя столами на пять мест[1].

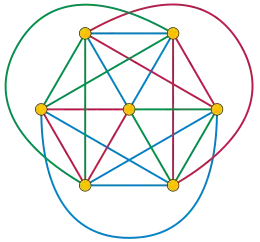
При формулировке задачи как задачи теории графов пары людей, сидящих рядом за конкретным обедом, могут быть представлены как объединение непересекающихся (по рёбрам) циклов ${\displaystyle C_{x}+C_{y}+C_{z}+\cdots }$ определённой длины, по одному циклу для каждого обеденного стола. Это объединение циклов является 2-регулярным графом, а любой 2-регулярный граф имеет такой вид. Если ${\displaystyle G}$ является таким 2-регулярным графом и имеет ${\displaystyle n}$ вершин, вопрос ставится так: можно ли полный граф ${\displaystyle K_{n}}$ представить как непересекающееся по рёбрам объединение копий графа ${\displaystyle G}$[1].

Чтобы решение существовало, общее число участников конференции (или, эквивалентно, полное число посадочных мест за столами, или общее число вершин заданных циклов) должно быть нечётным числом. За каждым обедом участник сидит рядом с двумя другими участниками, так что общее число соседей каждого участника должно быть чётным, а это возможно только при нечётном общем числе участников. Задачу, однако, можно распространить и на чётные значения ${\displaystyle n}$, если спрашивать для этих ${\displaystyle n}$, можно ли покрыть все рёбра полного графа за исключением совершенного паросочетания копиями заданного 2-регулярного графа. Подобно задаче о супружеских парах (другой математической задаче о рассаживании за обеденным столом), этот вариант задачи можно сформулировать в предположении, что ${\displaystyle n}$ участников обеда разбивается на ${\displaystyle n/2}$ супружеских пар, и что каждый участник должен пообедать ровно раз с каждым другим участником, за исключением супруги (супруга)[2].

Известны только следующие экземпляры задачи Обервольфаха, о которых известно, что они не имеют решения: ${\displaystyle OP(3^{2})}$, ${\displaystyle OP(3^{4})}$, ${\displaystyle OP(4,5)}$ и ${\displaystyle OP(3,3,5)}$. Широко распространено мнение, что все другие экземпляры решения имеют, но пока доказана разрешимость лишь специальных случаев.

Случаи, для которых известны решения:

• Все экземпляры ${\displaystyle OP(x^{y})}$, за исключением ${\displaystyle OP(3^{2})}$ и ${\displaystyle OP(3^{4})}$[3][4][5][6][2].
• Все экземпляры, в которых все циклы имеют чётную длину[3][7].
• Все экземпляры (кроме известных исключений) с ${\displaystyle n\leqslant 40}$[8].
• Все экземпляры для некоторых ${\displaystyle n}$, принадлежащих бесконечному набору простых чисел[9][10].
• Все экземпляры ${\displaystyle OP(x,y)}$, кроме известных исключений ${\displaystyle OP(3,3)}$ и ${\displaystyle OP(4,5)}$[11].

• Задача Киркмана о школьницах: группировки пятнадцати школьниц в ряды по три семью различными способами, так что каждая пара девочек оказывалась в тройке только раз, является частным случаем задачи Обервольфаха ${\displaystyle OP(3^{5})}$. Задача гамильтонова разложения полного графа ${\displaystyle K_{n}}$ является другим частным случаем ${\displaystyle OP(n)}$[7].

• Гипотеза Алспаха о разложении полного графа на циклы данных размеров связана с задачей Обервольфаха, но они не являются частными случаями друг друга. Если ${\displaystyle G}$ является 2-регулярным графом с ${\displaystyle n}$ вершинами, образованным непересекающимися циклами определённой длины, то решение задачи Обервольфаха для ${\displaystyle G}$ даёт разложение полного графа на ${\displaystyle (n-1)/2}$ копий каждого цикла графа ${\displaystyle G}$. Однако не любое разложение ${\displaystyle K_{n}}$ на такое число циклов каждого размера может быть сгруппировано на непересекающиеся циклы, которые образуют копии ${\displaystyle G}$, но, с другой стороны, не любой экземпляр гипотезы Алспаха вовлекает набор циклов, которые имеют ${\displaystyle (n-1)/2}$ копий каждого цикла.