Доминирующее множество рёбер

В теории графов доминирующее множество рёбер (или рёберное доминирующее множество) графа G = (V, E) — это подмножество D ⊆ E, такое, что любое ребро не из D смежно по меньшей мере одному ребру из D. На рисунках (a)–(d) приведены примеры доминирующих множеств рёбер (красные рёбра).

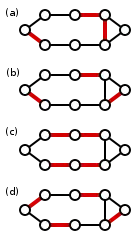
Примеры доминирующих множеств рёбер.

Наименьшее доминирующее множество рёбер — это доминирующие множества рёбер с наименьшим размером. На рисунках (a) и (b) представлены примеры наименьших доминирующих множеств рёбер (можно проверить, что для данного графа не существует доминирующего множества из двух рёбер).

Свойства
Дополнительные сведения: Доминирующее множество § Независимая доминация

Доминирующее множество рёбер для графа G является доминирующим множеством рёберного графа L(G), и наоборот.

Любое максимальное паросочетание всегда является рёберным доминирующим множеством. На рисунках (b) и (d) представлены примеры максимальных паросочетаний.

Более того, размер наименьшего доминирующего множества рёбер равен размеру наименьшего максимального паросочетания. Наименьшее максимальное паросочетание — это наименьшее доминирующее множество рёбер. Рисунок (b) даёт пример наименьшего максимального паросочетания. Наименьшее доминирующее множество рёбер не обязательно является наименьшим максимальным паросочетанием, что иллюстрирует рисунок (a). Однако, если задано наименьшее доминирующее множество рёбер D, легко найти наименьшее максимальное паросочетание с |D| рёбрами (см., например, статью Михалиса Яннаккиса и Фаницы Гаврилы[1]).

Алгоритмы и вычислительная сложность

Определение, существует ли доминирующее множество рёбер заданного размера для заданного графа, является NP-полной задачей (а потому нахождение наименьшего доминирующего множества рёбер является NP-трудной задачей). Михалиса Яннаккис и Фаница Гаврил[1] показали, что задача является NP-полной даже для двудольного графа с максимальной степенью вершин 3, а также для планарного графа с максимальной степенью вершин 3.

Существует простой аппроксимационный алгоритм полиномиального времени с коэффициентом аппроксимации 2 — находим любое максимальное паросочетание. Максимальное паросочетание является доминирующим множеством рёбер. Более того, максимальное паросочетание M может быть вдвое больше по размеру наименьшего максимального паросочетания, а наименьшее максимальное паросочетание имеет тот же размер, что и наименьшее доминирующее множество рёбер.

Можно также аппроксимировать с коэффициентом 2 рёберно-взвешенную версию задачи, но алгоритм существенно более сложен[2].

Хлебиков и Хлебикова[3] показали, что поиск с коэффициентом, лучшим (7/6), является NP-трудной задачей.

Примечания
  1. Yannakakis, Gavril, 1980.
  2. Fujito, Nagamochi, 2002.
  3. Chlebík, Chlebíková, 2006.

Литература
  • Giorgio Ausiello, Pierluigi Crescenzi, Giorgio Gambosi, Viggo Kann, Alberto Marchetti-Spaccamela, Marco Protasi. Complexity and Approximation: Combinatorial Optimization Problems and Their Approximability Properties. — Berin, Heidelberg, New York: Springer-Verlag, 2003. — ISBN 3-540-65431-3..
Наименьшее доминирующее множество рёбер (оптимизационная версия) — задача GT3 в Приложении B (стр. 370).
Наименьшее максимальное паросочетание (оптимизационная версия) — задача GT10 в Приложении B (стр. 374).
  • Miroslav Chlebík, Janka Chlebíková. Approximation hardness of edge dominating set problems // Journal of Combinatorial Optimization. — 2006. — Т. 11, вып. 3. — С. 279–290. — doi:10.1007/s10878-006-7908-0..
  • Michael R. Garey, David S. Johnson. Computers and Intractability: A Guide to the Theory of NP-Completeness. — W.H. Freeman, 1979. — ISBN 0-7167-1045-5..
Доминирующее множество рёбер (в версии разрешимости) обсуждается в задаче о доминирующем множестве, задаче GT2 в приложении A1.1.
Наименьшее максимальное паросочетнаие (в версии разрешимости) — задача GT10 в Приложении A1.1.
  • Mihalis Yannakakis, Fanica Gavril. Edge dominating sets in graphs // SIAM Journal on Applied Mathematics. — 1980. — Т. 38, вып. 3. — С. 364–372. — doi:10.1137/0138030. — ..
  • Toshihiro Fujito, Hiroshi Nagamochi. A 2-approximation algorithm for the minimum weight edge dominating set problem // Discrete Applied Mathematics. — 2002. — Т. 118, вып. 3. — С. 199–207. — doi:10.1016/S0166-218X(00)00383-8.

Ссылки
Наименьшее доминантное множество рёбер,
Наименьшее максимальное паросочетание.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.