Диаграмма Вольперта — Смита
Диаграмма Вольперта—Смита (круговая диаграмма полных сопротивлений, в англоязычной литературе — диаграмма Смита, в японской — диаграмма Мидзухаси-Смита) — круговая диаграмма, предназначенная для определения комплексных сопротивлений нагрузки линии по значениям коэффициента бегущей или стоячей волны и фазы коэффициента отражения. Названа в честь американского инженера Ф. Смита, предложившего диаграмму в 1939, и советского инженера А. Р. Вольперта, независимо описавшего её в 1940 году. Также в 1937 году японский инженер Т. Мидзухаси опубликовал статью[1] с изображением аналогичной диаграммы. Для практического использования диаграмма выпускается в планшете из прозрачного пластика, для удобства отсчёта на планшете имеется вращающаяся линейка, ось вращения которой проходит через центр диаграммы.
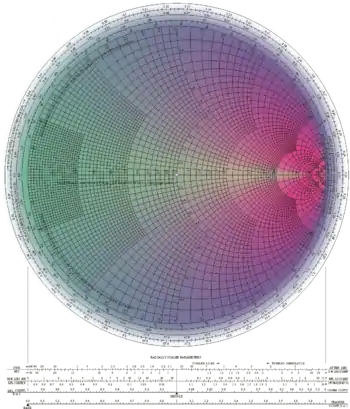
Описание диаграммы
Круговая диаграмма представляет собою две окружности — внешнюю и внутреннюю, внутри которых расположены два семейства ортогональных окружностей, соответствующих геометрическим местам точек нормированных сопротивлений R/ρ = const и Х/ρ = const, где:
- R — активное сопротивление нагрузки, Ом;
- X — реактивное сопротивление нагрузки, Ом;
- ρ — волновое сопротивление линии, Ом.
Применение нормированных сопротивлений позволяет применять диаграмму для измерения полных сопротивлений, включенных в линии передачи с любым волновым сопротивлением. На внешней окружности по направлению движения часовой стрелки отложены безразмерные значения отношения L0/λ, пропорциональные фазовому углу, на внутренней окружности те же значения отложены против движения часовой стрелки. Внешней окружностью следует пользоваться в том случае, когда расстояние до первого минимума L0 отсчитывается по направлению к генератору, внутренней — при отсчете L0 от генератора по направлению к нагрузке. По вертикальному диаметру отложены значения R/ρ, соответствующие проходящим через них окружностям равных нормированных активных сопротивлений. В местах пересечения окружностей равных нормированных реактивных сопротивлений с внешней окружностью помещены значения Х/ρ: в левой половине диаграммы отрицательные, в правой — положительные. На диаграмме штриховой линией нанесены окружности, проходящие через деления шкалы R/ρ, с центром в точке R/ρ = 1. По этим окружностям отсчитываются значения КБВ и КСВ, так как шкала нормированных активных сопротивлений от 0 до 1 на оси нулевых реактивных сопротивлений одновременно является шкалой КБВ, а от 1 до ∞ — шкалой КСВ.
Работа с диаграммой
Полное сопротивление определяют в следующем порядке. Из графика, полученного с помощью измерительной линии, характеризующего режим измеряемого тракта, определяют длину отрезка L0, длину волны λ и коэффициент KБВ или KСВ; вычисляют L0/λ. Центр диаграммы (точка R/ρ = 1) соединяют прямой линией (прозрачной линейкой) с внешней или внутренней окружностью, в зависимости от перемещения минимума к генератору или к нагрузке относительно положения его при коротком замыкании в точке L0/λ. На диаграмме отмечают точку пересечения прямой и окружности KБВ с двумя ортогональными окружностями R/ρ и Х/ρ. Значения R/ρ и Х/ρ, соответствующие этому пересечению, после умножения на ρ дают ответ на поставленную задачу, так как ZНагр = R + jX.
Литература
- 水橋東作. 四端子回路のインピーダンス変成と整合回路の理論 // 電気通信学会雑誌、1937. 第12号、P. 1053—1058. = Mizuhashi T. Theory of four-terminal impedance transformation circuit and matching circuit // The Journal of the Institute of Electrical Communication Engineers of Japan. December 1937. P.1053—1058.
- Smith P. H. Transmission Line Calculator // Electronics. Vol. 12, No. 1 (January 1939). P. 29—31.
- Вольперт А. Р. Номограмма для расчета длинных линий // Производственно-технический бюллетень НК.ЭП (Ленинград). 1940. № 2.
- Баскаков С. И. Радиотехнические цепи с распределенными параметрами. М: Высш. школа, 1980.
- Справочник по теоретическим основам радиоэлектроники / Под. ред. Б. Х. Кривицкого: в 2 т. М: Энергия, 1977.
- Сазонов Д. М., Гридин А. М., Мишустин Б. А. Устройства СВЧ. М.: Высш. школа, 1981.
Ссылки
Примечания
- 水橋東作. 四端子回路のインピーダンス変成と整合回路の理論 // 電気通信学会雑誌、1937. 第12号、P. 1053—1058.