Группа антисимметрии
Группа антисимметрии в теории симметрии — группа, состоящая из преобразований, которые могут менять не только геометрическое положение объекта, но и также его некоторую двухзначную характеристику. Такой двухзначной характеристикой может быть, например, заряд (плюс-минус), цвет (чёрный-белый), знак вещественной функции, направление спина (вверх-вниз).
Группы антисимметрии называются также группами магнитной симметрии, а также группами чёрно-белой симметрии. По аналогии с этими группами вводятся группы многоцветной симметрии (Беловские группы, так как они были предложены в работах академика Н. В. Белова), в которых каждая точка объекта характеризуется уже не двухзначным, а многозначным параметром (цветом).
Содержание
Операции и элементы антисимметрии
В дополнение к обычным операциям симметрии (вращение, отражение, инверсия, трансляция и их комбинации) добавляются операции антисимметрии — вращение с изменением цвета (антиповорот), отражение с изменением цвета (антиотражение), инверсия с изменением цвета (антиинверсия), трансляция с изменением цвета (антитрансляция) и так далее. Соответственно, можно говорить и об элементах антисимметрии, которые включают в себя операции антисимметрии.
Следует также учитывать операцию, которая не меняет положение объекта, но меняет цвет — операция антиотождествления или антитождества. Группы, в которых присутствует такая операция, называются серыми, так как там в каждой точке пространства совпадают белая и чёрная часть объекта. Такие группы получаются просто добавлением операции антитождества к классической группе симметрии и их число равно числу классических групп симметрии. Сами классические группы симметрии также являются частным случаем групп антисимметрии. Наибольший интерес представляют группы, которые не являются серыми, и в которых присутствуют как элементы симметрии, так и элементы антисимметрии (группы смешанной полярности). Элементы антисимметрии в этих группах могут быть только чётного порядка, так как элементы антисимметрии нечётного порядка содержат операцию антиотождествления. Например, ось антисимметрии 3 (порядок 3) невозможна в этих группах, а инверсионная ось 3 (порядок 6) — возможна.
Последовательное выполнение двух операций антисимметрии или 2n-кратное выполнение оодной операции антисимметрии дважды меняет знак, то есть в результате знак не меняется. Таким образом, произведение двух операций антисимметрии приводит к классической операции симметрии. Поэтому групп, которые содержат только элементы и операции антисимметрии, не существует. Более того, число операций (но не элементов) антисимметрии в точечных группах антисимметрии равно числу операций симметрии в классических (одноцветных) группах.
Точечные группы антисимметрии
Хотя понятие антисимметрии применимо к любым точечным группам, обычно рассматривают кристаллографические точечные группы антисимметрии. Всего существует 58 чёрно-белых групп, 32 классических полярных групп, и 32 серых нейтральных групп. Итого, 122 точечных групп антисимметрии. Ниже дана таблица всех 122 кристаллографических точечных групп антисимметрии. Обычно для их обозначения используются символы Германа-Могена, при этом элементы антисимметрии отмечаются символом соответствующего элемента симметрии со штрихом. В таблице даны сокращённые символы.
| Классические | Серые | Смешанной полярности | ||||
|---|---|---|---|---|---|---|
| 1 | 1' | |||||
| 1 | 11' | 1' | ||||
| 2 | 21' | 2' | ||||
| m | m1' | m' | ||||
| 2/m | 2/m1' | 2/m' | 2'/m | 2'/m' | ||
| 222 | 2221' | 2’2'2 | ||||
| mm2 | mm21' | m’m'2 | mm’2' | |||
| mmm | mmm1' | m’m'm' | mmm' | m’m'm | ||
| 4 | 41' | 4' | ||||
| 4 | 41' | 4' | ||||
| 4/m | 4/m1' | 4/m' | 4'/m' | 4'/m | ||
| 422 | 4221' | 4’22' | 42’2' | |||
| 4mm | 4mm1' | 4m’m' | 4’mm' | |||
| 42m | 42m1' | 42’m' | 4'2m' | 4'2’m | ||
| 4/mmm | 4/mmm1' | 4/m’m'm' | 4/m’mm | 4'/mmm' | 4'/m’m'm | 4/mm’m' |
| 3 | 31' = 3' | |||||
| 3 | 31' | 3' | ||||
| 32 | 321' | 32' | ||||
| 3m | 3m1' | 3m' | ||||
| 3m | 3m1' | 3m' | 3'm' | 3'm | ||
| 6 | 61' | 6' | ||||
| 6 | 61' | 6' | ||||
| 6/m | 6/m1' | 6/m' | 6'/m' | 6'/m | ||
| 622 | 6221' | 62’2' | 6’2'2 | |||
| 6mm | 6mm1' | 6m’m' | 6’mm' | |||
| 6m2 | 6m21' | 6m’2' | 6'm2' | 6'm’2 | ||
| 6/mmm | 6/mmm1' | 6'/mmm' | 6'/m’mm' | 6/m’m'm' | 6/m’mm | 6/mm’m' |
| 23 | 231' | |||||
| m3 | m31' | m'3' | ||||
| 432 | 4321' | 4’32' | ||||
| 43m | 43m1' | 4'3m' | ||||
| m3m | m3m1' | m'3'm' | m'3'm | m3m' | ||
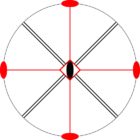
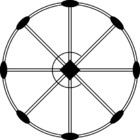
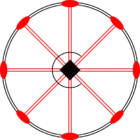
Стереографические проекции классических точечных групп и групп смешанной полярности.
Чёрным цветом обозначены элементы симметрии. Красным — элементы антисимметрии.
 |  |  | |||
|---|---|---|---|---|---|
 |  |  |  | ||
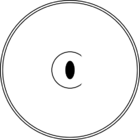 |  |  |  | ||
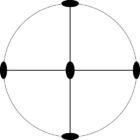 | 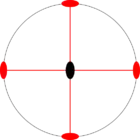 | 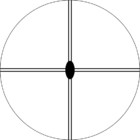 |  |  | |
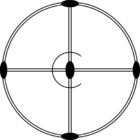 |  |  | 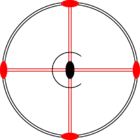 | ||
 |  |  |  | ||
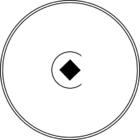 |  4/m' |  |  | ||
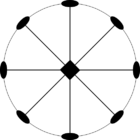 | 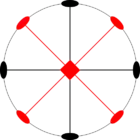 | 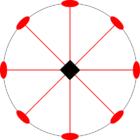 | |||
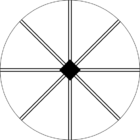 |  |  | |||
 | 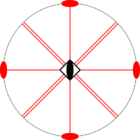 |  |  | ||
 |  |  |  |  |  |
 | 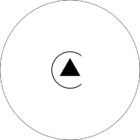 |  | |||
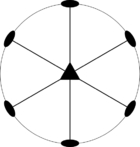 | 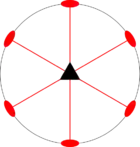 | 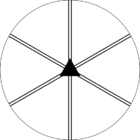 |  | ||
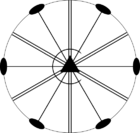 | 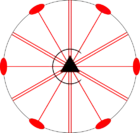 |  | 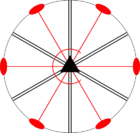 | ||
 |  | 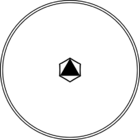 |  | ||
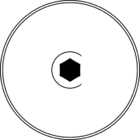 |  6/m' |  |  | ||
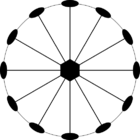 | 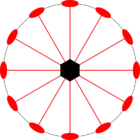 | 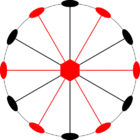 | |||
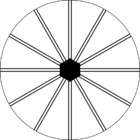 |  |  | |||
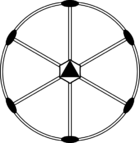 |  |  |  | ||
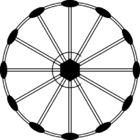 | 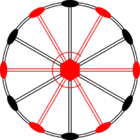 |  |  |  | 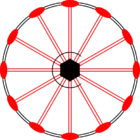 |
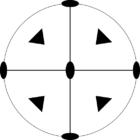 | 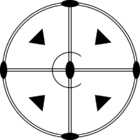 |  | |||
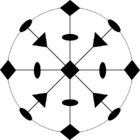 | 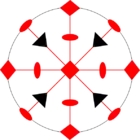 | 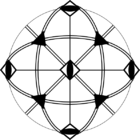 |  | ||
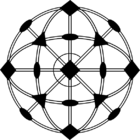 |  | 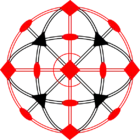 |  |
Пространственные группы антисимметрии (Шубниковские группы)
Всего существует 1191 чёрно-белых групп, 230 классических полярных групп, и 230 серых нейтральных групп. Итого — 1651 Шубниковская группа.
Другие кристаллографические группы антисимметрии
Число различных кристаллографических групп антисимметрии (в скобках дано число классических групп симметрии).[1][2]
| периодичность | Размерность пространства | ||||
|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | |
| 0 | 2 (1) | 5 (2) | 31 (10) | 122 (32) | 1202 (271) |
| 1 | 7 (2) | 31 (7) | 394 (75) | ||
| 2 | 80 (17) | 528 (80) | |||
| 3 | 1651 (230) | ||||
| 4 | 62227 (4894) | ||||
Литература
- А. В. Шубников. Симметрия и антисимметрия конечных фигур, Изд-во АН СССР, 1951.
- А. В. Шубников, В. А. Копцик. Симметрия в науке и искусстве. Издание 2-е, переработанное и дополненное. М., 1972.
- Ю. К. Егоров-Тисменко, Г. П. Литвинская, Ю. Г. Загальская, Кристаллография, МГУ, 1992.
- Ю. К. Егоров-Тисменко, Г. П. Литвинская, Теория симметрии кристаллов, ГЕОС, 2000. (доступно on-line http://geo.web.ru/db/msg.html?mid=1163834)
- В. А. Копцик, Шубниковские группы. М.: Изд-во МГУ, 1966.
- А. М. Заморзаев, Теория простой и кратной антисимметрии. Кишинев: Штиинца, 1976.
- Б. К. Вайнштейн, В. М. Фридкин, В. Л. Инденбом. Современная кристаллография. том 1. М.: Наука, 1979.
Примечания
- Б. К. Вайнштейн, В. М. Фридкин, В. Л. Инденбом. Современная кристаллография. том 1. М.: Наука, 1979, стр 176.
- Bernd Souvignier, The four-dimensional magnetic point and space groups, Z. Kristallogr. 221 (2006) 77-82