Граф Хэмминга
Графы Хэмминга — это специальный класс графов, названных именем Ричарда Хэмминга и используемых в некоторых областях математики и информатики.
| Граф Хэмминга | |
|---|---|
 | |
| Назван в честь | Ричарда Хэмминга |
| Вершин | |
| Рёбер | |
| Диаметр | |
| Спектр | |
| Свойства |
-регулярный вершинно транзитивный дистанционно регулярный [1] |
Определение
Пусть S — множество из q элементов, а d — положительное число. Граф Хэмминга H(d,q) имеет множество вершин Sd, множество упорядоченных d-кортежей элементов множества S (последовательности длины d элементов из S). Две вершины смежны, если они отличаются ровно одной координатой, то есть если расстояние Хэмминга равно единице. Граф Хэмминга H(d,q) равен прямому произведению d полных графов Kq [1].
В некоторых случаях графы Хэмминга могут определяться как прямое произведение полных графов, которые могут иметь различные размеры[2]. В отличие от графов H(d,q), эти графы более широкого класса не будут обязательно дистанционно регулярными, но остаются регулярными и вершинно транзитивными.
Специальные случаи
- H(2,3) является обобщённым четырёхугольником G Q (2,1)[3]
- H(1,q) является полным графом Kq[4].
- H(2,q) является графом-решёткой Lq,q, а также ладейным графом [5].
- H(d,1) является графом с одной вершиной K1
- H(d,2) является графом гиперкуба Qd[1]
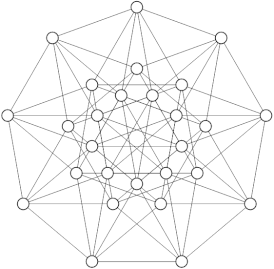
- H(3,3) является графом единичных расстояний с n=27 вершинами и n4/3=81 рёбрами (на рисунке)
Приложения
Графы Хэмминга интересны их связью с кодами с исправлением ошибок[6] и схемами отношений[7]. Они также приняты в качестве сетевой топологии в распределённых вычислениях[4].
Вычислительная сложность
Можно проверить, является ли граф графом Хэмминга, и если является, найти разметку вершин кортежами, которая реализует граф Хэмминга, за линейное время[2].
Примечания
- Brouwer, Haemers, 2012, с. 178.
- Imrich, Klavžar, 2000, с. 104–106.
- (Blokhuis, Brouwer, Haemers 2007). См. примечание на стр. 300.
- Dekker, Colbert, 2004, с. 359–368.
- Bailey, Cameron, 2011, с. 209–242.
- Sloane, 1989, с. 11–20.
- (Koolen, Lee, Martin 2010) На стр. 224 авторы пишут, что «тщательное изучение полных регулярных кодов в графах Хэмминга является центральным моментом при изучении ассоциативных схем».
Литература
- Andries E. Brouwer, Willem H. Haemers. Spectra of graphs. — New York: Springer, 2012. — С. 178. — (Universitext). — ISBN 978-1-4614-1938-9. — doi:10.1007/978-1-4614-1939-6.
- Wilfried Imrich, Sandi Klavžar. Product graphs. — Wiley-Interscience, New York, 2000. — С. 104—106. — (Wiley-Interscience Series in Discrete Mathematics and Optimization). — ISBN 0-471-37039-8.
- Aart Blokhuis, Andries E. Brouwer, Willem H. Haemers. On 3-chromatic distance-regular graphs // Designs, Codes and Cryptography. — 2007. — Т. 44, вып. 1—3. — С. 293—305. — doi:10.1007/s10623-007-9100-7.
- Anthony H. Dekker, Bernard D. Colbert. Proceedings of the 27th Australasian conference on Computer science - Volume 26. — Darlinghurst, Australia, Australia: Australian Computer Society, Inc., 2004. — С. 359—368. — (ACSC '04).
- Robert F. Bailey, Peter J. Cameron. Base size, metric dimension and other invariants of groups and graphs // Bulletin of the London Mathematical Society. — 2011. — Т. 43, вып. 2. — С. 209—242. — doi:10.1112/blms/bdq096.
- N. J. A. Sloane. Unsolved problems in graph theory arising from the study of codes // Graph Theory Notes of New York. — 1989. — Т. 18. — С. 11—20.
- Jacobus H. Koolen, Woo Sun Lee, William J. Martin. Combinatorics and graphs. — Providence, RI: Amer. Math. Soc., 2010. — Т. 531. — С. 223—242. — (Contemp. Math.). — doi:10.1090/conm/531/10470.
Ссылки
- Weisstein, Eric W. Hamming Graph (англ.) на сайте Wolfram MathWorld.
- Brouwer, Andries E. Hamming graphs.