Графы Чана
Графы Чана — это набор из трёх 12-регулярных неориентированных графов, каждый с 28 вершинами и 168 рёбрами. Все они сильно регулярны и имеют те же параметры и спектр, что и рёберный граф L(K8) полного графа K8. Графы Чана названы именем Ли-Чиена Чана, который доказал, что, за исключением этих трёх графов, любой рёберный граф полного графа единственным образом определяется его параметрами сильно регулярного графа[1].
| графы Чана | |
|---|---|
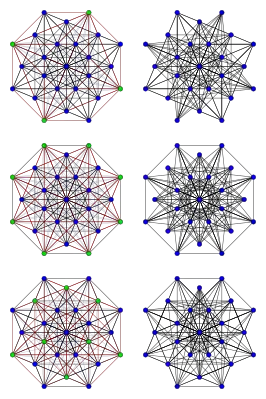 Три графа Чана (справа) и переключающие множества, генерирующие их из рёберного графа L(K8) (зелёные вершины слева) | |
| Назван в честь | Ли-Чиена Чана |
| Вершин | 28 |
| Рёбер | 168 |
| Радиус | 2 |
| Диаметр | 2 |
| Обхват | 3 |
| Автоморфизмы | 96360384 |
| Свойства | Сильно регулярный |
Связь с графами
Каждый из этих трёх графов может быть получен переключением графа из . То есть выбирается подмножество S вершин графа , каждое ребро, которое соединяет вершину из S с вершиной не из S в графе , удаляется и добавляются рёбра для каждой пары вершин (снова одна принадлежит S, а другая не принадлежит), которые ранее не были соединены ребром. Среди графов, которые могут быть образованы таким образом, находятся графы Чана.
См. также
- Граф Шрикханде, похожее исключение единственности параметров сильно регулярных графов
Примечания
- Chang, 1959, с. 604–613.
Литература
- Chang Li-Chien. The uniqueness and non-uniqueness of the triangular association schemes // Science Record (Peking). — 1959. — Т. 3.