Борелли, Джованни Альфонсо

Джова́нни Альфо́нсо Боре́лли (итал. Giovanni Alfonso Borelli; 28 января 1608, Неаполь — 31 декабря 1679, Рим) — итальянский учёный-универсал времени Научной революции XVII века. Автор трудов по физике, медицине, астрономии, геологии, математике, механике. Основоположник биомеханики. Один из первых учёных, рассмотревших проблему динамики планетных движений и проложивших Ньютону дорогу для открытия закона всемирного тяготения.

В Википедии есть статьи о других людях с фамилией Борелли.
Джованни Альфонсо Борелли
Giovanni Alfonso Borelli
Дата рождения 28 января 1608(1608-01-28)
Место рождения Неаполь
Дата смерти 31 декабря 1679(1679-12-31) (71 год)
Место смерти Рим
Страна  Неаполитанское королевство
Научная сфера физиология и математика
Место работы Пизанский университет
Альма-матер
Научный руководитель Бенедетто Кастелли
Ученики Michelangelo Fardella[d] и Alessandro Marchetti[d]
Известен как автор формулы закона всемирного тяготения, основоположник биомеханики
 Медиафайлы на Викискладе

Биография

Родился в Кастель Нуово (предместье Неаполя) в семье испанского солдата, женатого на итальянке. Свои труды позже подписывал фамилией матери: Борелли.

Сведения о его ранней биографии скудны. Учился в Риме, изучал медицину и математику у ученика Галилея Кастелли (вместе с Торричелли). С 1635 года работал в университете Мессины, с 1649 года — профессор математики. Примерно в начале 1640-х лично познакомился с Галилеем.

В 1656 году Борелли занял кафедру математики в Пизанском университете[2]. Здесь он познакомился с врачом Марчелло Мальпиги, который одним из первых начал исследования с помощью микроскопа. Борелли также увлёкся этой тематикой и получил ряд ценных результатов.

В 1668 году Борелли вернулся в Мессину, но вскоре на него пали подозрения в участии в политическом заговоре, и он вынужден был бежать из города. Остаток жизни он провёл в бедности, работая школьным учителем в Риме. Его главный труд по биомеханике, «О движении животных», был издан посмертно (1680).

Научная деятельность

Биомеханика
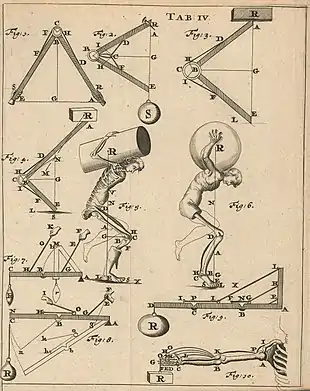
Скелетно-мышечная схема из книги Борелли

Борелли считается основоположником биомеханики. Его двухтомный труд «О движении животных» (лат. De Motu Animalium) рассматривает организм животного с точки зрения математической теории механизмов. Особенно подробно он исследовал работу мускулов. Например, сердце он рассматривал как насос с клапанами, легкие — как два меха, а процесс ходьбы — как целенаправленное перемещение центра тяжести, сопровождаемое мерами по восстановлению равновесия.

Борелли исследовал как статику, так и динамику тела, оценил силу, развиваемую мускулами при разных видах активности (ходьба, бег, прыжки, поднятие тяжестей). Он рассмотрел также полёт птиц, плавание рыб и скольжение червей.[3] Эта работа неоднократно переиздавалась и оказала большое влияние на теоретическую медицину.

Астрономия

Борелли продолжил систематическое изучение открытых Галилеем спутников Юпитера. В своей книге «Теория Медичийских планет» (1666) он сделал исключительно важный на тот момент вывод, что для них, как и для планет, выполняются законы Кеплера. В этой же книге он одним из первых сформулировал несовершенный, но принципиально верный вариант закона всемирного тяготения, предположив, что движение планет происходит в обстановке равновесия между притяжением к Солнцу и некоторой центробежной силой, аналогичной той, которая выбрасывает камень из пращи. Борелли так описал механизм движения под действием тяготения:

Предположим, что планета стремится к Солнцу и в то же время своим круговым движением удаляется от этого центрального тела, лежащего в середине круга. Если обе противоположные силы равны между собой, то они должны уравновешиваться. Планета не будет в состоянии ни приблизиться к Солнцу, ни отойти от него дальше известных пределов, и в таком равновесии будет продолжать своё обращение около Солнца[4].

В книге ясно видно, насколько плодотворным оказалось применение к модели Кеплера «новой механики» Галилея, которая оказалась способной пусть не количественно, но качественно верно объяснить (не раскрытую Кеплером) причину движения планет. Борелли правильно объясняет и причину отклонения планетной орбиты от круга: форма орбиты зависит от начального соотношения двух указанных сил. Вместе с тем, по мнению Борелли, от Солнца исходит ещё одна сила, продвигающая планету по орбите, возникающая при воздействии на планету световых лучей вращающегося Солнца[5].

Примерно в эти же годы интенсивные исследования в области динамики планетных движений проводили Кристофер Рен, Роберт Гук и Исаак Ньютон; последний, завершив математизацию основ небесной механики, назвал Борелли в числе своих предшественников[6].

Другие научные достижения
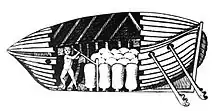
Подводная лодка, описанная в De Motu Animalium

Борелли впервые рассмотрел возможность создания дыхательного аппарата для подводных исследований.[7] Он также изучал под микроскопом состав крови животных и работу устьиц растений.

В 1660 году Борелли и Вивиани провели довольно точное измерение скорости звука и получили значение, соответствующее примерно 350 м/сек. Более ранние измерения, выполненные Гассенди, оценивали скорость звука в 478 м/сек (современная оценка: 331,3 м/сек при 0 °C).

Борелли по-видимому, первый заметил, что атмосферное давление связано с погодой: «Когда в каком-то районе надвигается длительный дождь, тогда ртуть в трубке поднимается на несколько градусов против обычного уровня; когда же дождь уже идёт, уровень ртути в трубке обычно падает, и эти различия уровня ртути не столь уж ничтожны». Борелли отметил (1670), что высота подъёма жидкости по капиллярной трубке обратно пропорциональна диаметру капилляра.[8]

Борелли издал с собственными подробными комментариями «Начала» Евклида (1658) и три книги «Конических сечений» Аполлония (1661).

Научные труды
  • Причины лихорадки (Della cagioni delle febbri maligne, Пиза, 1658)
  • Евклид восстановленный (Euclides Restitutus, Пиза, 1658)
  • Конические сечения Аполлония Пергского, книги V—VII (Apollonii Pergaei Conicorum libri v., vi. et vii, Флоренция, 1661)
  • Теория Медичийских планет (Theoricae Mediceorum planetarum ex causis physicis deductae, Флоренция, 1666)
  • De vi percussionis (Болонья, 1667)
  • Meteorologia Aetnea (Реджо, 1669)
  • De motionibus naturalibus a gravitate pendentibus (Болонья, 1670).
  • О движении животных (De Motu Animalium, Рим, 1680)

Примечания
  1. Математическая генеалогия (англ.) — 1997.
  2. Борелли, Джованни-Альфонсо // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
  3. Д. Антисери, Дж. Реале. Западная философия от истоков до наших дней. — СПб.: Пневма, 2002. — Т. II. От Возрождения до Канта. — С. 265—266. — ISBN 5-9014151-05-4.
  4. Спасский Б. И. История физики. — М.: Высшая школа, 1977. — Т. 1. — С. 141.
  5. Черняк, 2003, с. 115-117.
  6. Вавилов С. И. Исаак Ньютон. 2-е изд. М.-Л.: Изд-во АН СССР, 1945. Глава 9, с.109-124.
  7. Quick, D. A History Of Closed Circuit Oxygen Underwater Breathing Apparatus (англ.) // Royal Australian Navy, School of Underwater Medicine. : journal. — 1970. — Vol. RANSUM—1—70. Архивировано 9 мая 2008 года.
  8. Розенбергер Ф. История физики, пер. с нем., 2 изд., ч. 2, М.—Л., 1937.

Литература

Ссылки


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.