Алиса и Боб

Алиса и Боб — имена, обычно использующиеся в качестве условных обозначений взаимодействующих агентов или архетипичных символов в таких областях, как криптография, компьютерная безопасность и физика. Используются для удобства объяснения работы сетевых протоколов: фраза «Алиса посылает Бобу сообщение, зашифрованное его открытым ключом» гораздо легче воспринимается, чем «сторона А посылает стороне Б сообщение, зашифрованное открытым ключом стороны Б». Со временем сформировались традиции, какими именами обозначать каких участников процесса.

Важно понимать, что «Алиса», «Боб» и т. п. обозначают не обязательно людей, а вообще агентов, независимо от их реализации: это могут быть, например, компьютерные программы, действующие от имени людей.

Список символов
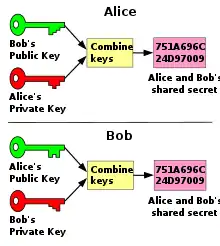
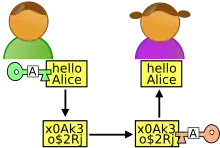
Пример: генерация общего секретного ключа
Пример: шифрование с открытым ключом

В основном, данный список составлен на основании книги «Прикладная криптография» Брюса Шнайера (Applied Cryptography by Bruce Schneier)[1]. Алиса и Боб — архетипы в области криптографии; Ева — более общее имя.

  • Алиса и Боб (Alice and Bob) — Наиболее часто Алиса хочет послать сообщение Бобу. Эти имена были использованы Роном Ривестом (Ron Rivest) в 1978 году в журнале «Communications of the ACM» в статье «A Method for Obtaining Digital Signatures and Public-Key Cryptosystems»[2]. Ривест отрицает, что эти имена имеют отношение к фильму 1969 года «Боб и Кэрол, Тед и Элис», как предполагалось некоторыми.
  • Кэрол, Карлос или Чарли (Carol, Carlos or Charlie) — выступают в качестве третьего участника соединения.
  • Чак (Chuck) — посторонний, обычно злоумышленник.
  • Крейг (Craig) — взломщик паролей (cracker), обычно встречается в ситуации с хранимыми хэшами.
  • Дейв (Dave) — четвёртый участник (и так далее по алфавиту).
  • Ева (Eve) — пассивный злоумышленник, от англ. eavesdropper (подслушивающий). Она может прослушивать сообщения между Алисой и Бобом, но она не может влиять на них. В квантовой криптографии Ева может представлять окружающую среду.
  • Мэллори (Mallory, от malicious) или Труди (Trudy, от intruder) — активный злоумышленник; в отличие от Евы, Мэллори может изменять сообщения, воспроизводить старые сообщения, подменять сообщения и так далее.
  • Пегги (Peggy), прувер (prover) и Виктор (Victor), контролирующий (verifier) — третьи лица, доказывающие, что транзакция произошла. Они встречаются, в частности, в доказательстве с нулевым разглашением.
  • Трент (Trent), доверенный арбитр — своего рода нейтральная третья сторона, чья точная роль изменяется в зависимости от стадии обсуждения протокола.
  • Уолтер (Walter) — надзиратель, может быть необходим для охраны Алисы и Боба, в зависимости от обсуждаемого протокола.

Схожие типовые условные имена применяются в некоторых других областях:

  • Артур и Мерлин (Arthur and Merlin) — в интерактивной системе доказательств Мерлин имеет неограниченную вычислительную способность, а следовательно, является могучим волшебником. Он утверждает истинность высказывания, а Артур, мудрый король, ставит его под сомнение. Эти два символа дают название двум классам сложности — MA и AM.
  • Пол и Кэрол (Paul and Carole) — эти имена были введены для решения задачи о двадцати вопросах (Twenty Questions, 20Q), где Пол, задающий вопросы, выступал в роли Пала Эрдёша, а Кэрол, которая ему отвечала, была анаграммой оракула (Carole и oracle)[3]. В дальнейшем они были использованы в некоторых комбинаторных играх соответственно в ролях Пушера и Чузера (Pusher and Chooser).

См. также

Примечания
  1. Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = Applied Cryptography. Protocols, Algorithms and Source Code in C. — М.: Триумф, 2002. — 816 с. — 3000 экз. — ISBN 5-89392-055-4.
  2. Rivest R., Shamir A., Adleman L. A method for obtaining digital signatures and public-key cryptosystems (англ.) // Commun. ACM — [New York]: Association for Computing Machinery, 1978. — Vol. 21, Iss. 2. — P. 120—126. — ISSN 0001-0782; 1557-7317 — doi:10.1145/359340.359342
  3. Spencer, Joel & Winkler, Peter (1992), Three Thresholds for a Liar, Combinatorics, Probability and Computing Т. 1 (01): 81–93, doi:10.1017/S0963548300000080, <http://math.dartmouth.edu/~pw/papers/3thresh.ps>

Литература
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.