Алгоритм Тарьяна

Алгоритм Тарьяна — алгоритм поиска компонент сильной связности в орграфе, работающий за линейное время.

Анимация алгоритма Тарьяна


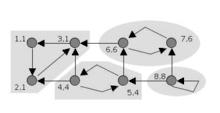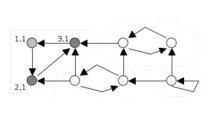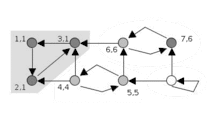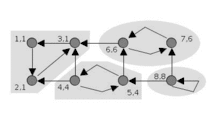
Этот алгоритм основан на том, что:

  1. Вершины рассматриваются в обратном топологическом порядке, поэтому в конце рекурсивной функции для исходной вершины не будет встречено ни одной вершины из той же сильной компоненты, так как все вершины, достижимые из исходной, уже обработаны.
  2. Обратные связи в дереве дают второй путь из одной вершины в другую и связывают сильные компоненты.

Неформальное описание алгоритма

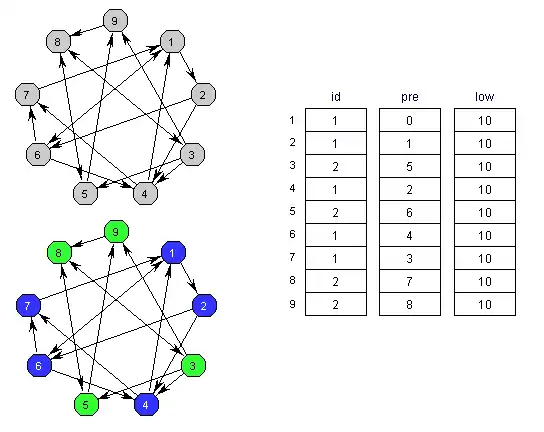
Алгоритм Тарьяна можно понимать как вариацию алгоритма поиска в глубину, в котором при посещении вершины и окончании обработки вершины выполняются дополнительные действия. Посещение вершины происходит при движении от корня к листьям, а окончание обработки вершины — на обратном пути. При посещении вершины она проталкивается во вспомогательный стек, а выталкивается при окончании обработки[1].

Индексы компонент связности всех вершин хранятся в векторе id, индексированном номерами вершин. Вектор low отслеживает вершину с наименьшим номером в прямом порядке обхода, достижимую из каждого узла через последовательность прямых связей, за которыми следует одна восходящая связь. Воспользовавшись поиском в глубину с тем, чтобы рассматривать вершины в обратном топологическом порядке, мы вычисляем для каждой вершины v максимальную точку, достижимую через обратную связь из предшественника (low[v]). Когда для вершины v выполняется pre[v]=low[v], мы выталкиваем её из стека, а также все вершины выше её и всем им присваиваем номер следующей компоненты.

Время работы

Алгоритм имеет временну́ю сложность , где  — количество рёбер, а  — вершин графа[1].

См. также

Алгоритм нахождения компонент сильной связанности — аналогичный алгоритм, использующий поиск в глубину.

Примечания
  1. Джереми Сик и др., 2006.

Ссылки

Литература
  • Tarjan R. E. Depth-first search and linear graph algorithms (англ.) // SIAM Journal on Computing. — 1972. — Vol. 1, no. 2. — P. 146–160. — doi:10.1137/0201010.
  • Роберт Седжвик. Алгоритмы на графах = Graph algorithms. — 3-е изд. — Россия, Санкт-Петербург: «ДиаСофтЮП», 2002. — С. 496. — ISBN 5-93772-054-7.
  • Джереми Сик, Лай-Кван Ли, Эндрю Ламсдэйн. C++ Boost Graph Library. — Питер, 2006. — С. 202—205. — 304 с. — ISBN 5-469-00352-3.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.