Алгоритмы быстрого возведения в степень по модулю

Алгоритмы быстрого возведения в степень по модулю — разновидность алгоритмов возведения в степень по модулю, широко использующихся в различных криптосистемах, для ускорения вычислительных операций с большими числами.

Метод с использованием Китайской теоремы об остатках

Описание метода

Пусть требуется вычислить $S=x^{a}{\bmod {n}}$ , где числа $x,a,n$ достаточно большие и пусть модуль может быть разложен на простые делители $n=p_{1}p_{2}...p_{j}$ . Тогда для быстрого возведения в степень по модулю можно воспользоваться китайской теоремой об остатках и решить систему уравнений (предварительно посчитав вычеты $x^{a}\equiv r_{i}{\pmod {p_{i}}}$ с использованием теоремы Ферма, где $i=1,2,...,j$ ):

${\begin{cases}x^{a}\equiv r_{1}{\pmod {p_{1}}},\qquad 0\leqslant r_{1}<p_{1}\\x^{a}\equiv r_{2}{\pmod {p_{2}}},\qquad 0\leqslant r_{2}<p_{2}\\\qquad ......\qquad \qquad \qquad ......\\x^{a}\equiv r_{j}{\pmod {p_{j}}},\qquad 0\leqslant r_{j}<p_{j}\\\end{cases}}$

Заменив $x^{a}$ на $t$ для удобства, решаем систему относительно $t$ и получаем $S$ .

Пример

Пусть требуется вычислить $S=3^{5}{\bmod {3}}0$

${\begin{cases}t=3^{5}\equiv 1{\pmod {2}}\\t=3^{5}\equiv 0{\pmod {3}}\\t=3^{5}\equiv 3{\pmod {5}}\\\end{cases}}$

Представим систему в виде

${\begin{cases}t=3^{5}=1+2u\\t=3^{5}=0+3v\\t=3^{5}=3+5w\\\end{cases}}$

Подставив t из первого уравнения во второе, получим $1+2u\equiv 0{\pmod {3}}$ , тогда $2u\equiv 2{\pmod {3}}$ , или $u\equiv 1{\pmod {3}}$ , или $u=1+3h$ ;

подставив затем t из первого уравнения в третье с учетом выражения для $u$ получим $1+2(1+3h)\equiv 3{\pmod {5}}$ или $6h\equiv 0{\pmod {5}}$ , тогда $h=0{\pmod {5}}$ ;

тогда $t=3^{5}\equiv 1+2(1+3\cdot 0)\equiv 3{\pmod {5}}$ следовательно, $S=3^{5}{\bmod {5}}=3$ ;

Применение

Значительный выигрыш от данного алгоритма можно получить при выполнении умножения. Умножение будет проводится в два раза быстрее при использовании данного алгоритма.

Вычислительная сложность

Данный метод позволяет сократить количество вычислений в $3-4$ раза. Пусть $a$ имеет длину $k$ бит. При обычном возведении в степень затратится около $3k/2$ умножений по модулю. Пусть мы хотим вычислить $(x^{a}{\bmod {p}},x^{a}{\bmod {q}})$ . Сокращая $a$ на $p-1$ и $q-1$ задача сводится к вычислению $(x^{a{\bmod {(}}p-1)}{\bmod {p}},x^{a{\bmod {(}}q-1)}{\bmod {q}})$ . Каждая степень в данной записи имеет длину $k/2$ . Поэтому каждая операция возведения в степень потребует $3k/4$ операций. Итого потребуется $2\cdot 3k/4=3k/2$ умножений по модулю простого числа $p$ или $q$ вместо изначального умножения по модулю $n$ .

Метод повторяющихся возведения в квадрат и умножения

Пример блок-схемы метода повторяющихся возведения в квадрат и умножения

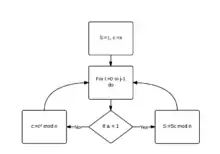
Описание метода

Пусть требуется вычислить $x^{a}{\bmod {n}}$ . Представим степень $a=a_{j-1}2^{j-1}+a_{j-2}2^{j-2}+...+a_{2}2^{2}+a_{1}2^{1}+a_{0}$ , где $a_{j}=(0,1)$

Представим $x^{a}{\bmod {n}}$ в виде:

$x^{a}{\bmod {n}}=x^{a_{j-1}2^{j-1}+a_{j-2}2^{j-2}+...+a_{2}2^{2}+a_{1}2^{1}+a_{0}}{\bmod {n}}=$

$=(x^{2})^{a_{j-1}2^{j-2}+a_{j-2}2^{j-3}+...+a_{1}2^{0}}x^{a_{0}}{\bmod {n}}=$

$=((x^{2})^{2})^{a_{j-1}2^{j-3}+a_{j-2}2^{j-4}+...+a_{2}2^{0}}(x^{2})^{a_{1}}x^{a_{0}}{\bmod {n}}=$

$=(...((x^{2})^{2}...)^{2})^{a_{j-1}}...(x^{8})^{a_{3}}(x^{4})^{a_{2}}(x^{2})^{a_{1}}x^{a_{0}}{\bmod {n}}$

Далее высчитывается значение выражения $x^{2}{\bmod {n}}$ и проводится замена в преобразованном выражении.

Данная операция производится до тех пор пока не будет найден результат.

Пример

Пусть требуется вычислить $249^{321}{\bmod {4}}99$ . Представим степень в виде $321=256+64+1=2^{8}+2^{6}+2^{0}$ . Представим $249^{321}{\bmod {4}}99$ в виде $249^{321}{\bmod {4}}99=249^{2^{8}+2^{6}+2^{0}}{\bmod {4}}99=$

$=(((((((249^{2})^{2})^{2})^{2})^{2})^{2})^{2})^{2}(((((249^{2})^{2})^{2})^{2})^{2})^{2}249{\bmod {4}}99=[249^{2}\equiv 125({\bmod {4}}99)]=$

$=((((((125^{2})^{2})^{2})^{2})^{2})^{2})^{2}((((125^{2})^{2})^{2})^{2})^{2}249{\bmod {4}}99=[125^{2}\equiv 156({\bmod {4}}99)]=$

$=(((((156^{2})^{2})^{2})^{2})^{2})^{2}(((156^{2})^{2})^{2})^{2}249{\bmod {4}}99=[156^{2}\equiv 384({\bmod {4}}99)]=$

$=((((384^{2})^{2})^{2})^{2})^{2}((384^{2})^{2})^{2}249{\bmod {4}}99=[384^{2}\equiv 251({\bmod {4}}99)]=$

$=(((251^{2})^{2})^{2})^{2}(251^{2})^{2}249{\bmod {4}}99=[251^{2}\equiv 127({\bmod {4}}99)]=$

$=((127^{2})^{2})^{2}127^{2}249{\bmod {4}}99=[127^{2}\equiv 161({\bmod {4}}99)]=$

$=(161^{2})^{2}161*249{\bmod {4}}99=[161^{2}\equiv 472({\bmod {4}}99)]=$

$=472^{2}161*249{\bmod {4}}99=[472^{2}\equiv 230({\bmod {4}}99)]=$

$=230*161*249{\bmod {4}}99=447$

Применение

Если $n$ — простое или является произведением двух больших простых чисел, то обычно используют метод повторяющихся возведения в квадрат и умножения. Однако, если $n$ — составное, то обычно используют это метод вместе с китайской теоремой об остатках.

Вычислительная сложность

Средняя сложность данного алгоритма равна $1,5a$ операций умножения двух $a$ -битовых чисел плюс $1,5a$ операций деления $2a$ -битовых чисел на $a$ -битовое число. Для $1000$ -битовых и более длинных чисел данный алгоритм выполняется на ЭВМ достаточно быстро.

Метод Монтгомери возведения в степень

История

Данный метод был предложен 1985 году Питером Монтгомери для ускорения выполнения модульного возведения в степень.

Описание метода

В этом методе каждому числу $x$ ставится в соответствие некоторый образ $F(x)$ и все вычисления производятся с $F(x)$ , а в конце производится переход от образа к числу.

Теорема(Монтгомери).

Пусть $N,R$ — взаимно простые положительные целые числа, а $N'=(-N^{-1}){\bmod {R}}$ . Тогда для любого целого $x$ число $y=x+N((xN'){\bmod {R}})$ делится на $R$ , причем $y/R\equiv xR^{-1}({\bmod {N}})$ . Более того, если $0\leqslant x<RN$ , то разность $y/R-((xR^{-1}){\bmod {N}})$ равна либо $0$ , либо $N$ .

Данная теорема позволяет вычислить оптимальным способом величину $(xR^{-1}){\bmod {N}}$ для некоторого удобно выбранного $R$ .

Определение 1. Для чисел $R$ , $N$ , $x$ , таких что НОД $(R,N)=1$ и $0\leqslant x<N$ , назовем $(R,N)$ — остатком числа $x$ величину ${\overline {x}}=(xR){\bmod {N}}$ .

Определение 2. Произведением Монтгомери двух целых чисел $a$ , $b$ называется число $M(a,b)=abR^{-1}{\bmod {N}}$

Теорема (правила Монтгомери). Пусть числа $R$ , $N$ взаимно просты, и $0\leqslant a,b<N$ . Тогда $a{\bmod {N}}=M({\overline {a}},1)$ и $M({\overline {a}},{\overline {b}})={\overline {ab}}$

То есть, для наглядности, запишем выражение для возведения $x$ в $3$ степень: $M(M(M({\overline {x}},{\overline {x}}),{\overline {x}}),1)=x^{3}{\bmod {N}}$

Алгоритм(Произведение Монтгомери). Пусть заданы целые числа $0\leqslant c,d<N$ , где $N$ нечетно, а $R=2^{s}>N$ . Этот алгоритм возвращает $M(c,d)$ .

1.[Функция M Монтгомери]

M(c,d)

{

x=cd

;

z=y/z

;

//В соответствии с теоремой(Монтгомери).

2.[Поправить результат]

if

(z\geqslant N)z=z-N

;

return

z

;

}

Алгоритм(Метод Монтгомери возведения в степень). Пусть заданы числа $0\leqslant x<N$ , $y>0$ , и $R$ выбрано так же, как для алгоритма(Произведение Монтгомери). Этот алгоритм возвращает $x^{y}{\bmod {N}}$ . Через $(y_{0},...,y_{D-1})$ мы обозначаем двоичные биты $y$ .

1.[Начальная установка]

{\overline {x}}=(xR){\bmod {N}}

;

//С помощью какого-либо метода деления с остатком.

{\overline {p}}=R{\bmod {N}}

;

//С помощью какого-либо метода деления с остатком.

2.[Схема возведения в степень]

for

(D-1\geqslant j\geqslant 0)

{

{\overline {p}}=M({\overline {p}},{\overline {p}})

;

//с помощью алгоритма(произведение Монтгомери).

if

(y_{i}==1){\overline {p}}=M({\overline {p}},{\overline {x}})

;

}

//Теперь

{\overline {p}}

равняется

{\overline {x}}^{y}

.

3.[Окончательное получение степени]

M({\overline {p}},1)

;

В итоге получаем образ ${\overline {x}}=xR{\bmod {N}}$ , от которого мы можем получить конечный результат $x={\overline {x}}R^{-1}{\bmod {N}}$ , причем выражение $R^{-1}{\bmod {N}}$ вычислено заранее. Для произведения двух чисел результат будет выглядеть как $z={\overline {z}}R^{-1}{\bmod {N}}={\overline {x}}{\overline {y}}R^{-1}{\bmod {N}}\equiv {\frac {{\overline {x}}{\overline {y}}-({\overline {x}}{\overline {y}}(N^{-1}{\bmod {R}}){\bmod {R}})N}{R}}{\bmod {N}}$

Пример

Пусть $N=11$ , $b=R=2^{5}=32>N$ и хотим перемножить два числа $x=3$ и $x=3$ (т.е. возвести $x$ в квадрат)

$3$ имеет образ $3\cdot R{\bmod {N}}=96{\bmod {1}}1=8$

(для проверки $9$ имеет образ $9\cdot R{\bmod {N}}=288{\bmod {1}}1=2$ )

Перемножаем образы:

$w={\overline {x}}\cdot {\overline {x}}=64$ ,

Производим переход от образа умножения к искомому прообразу

$q=N^{-1}{\bmod {R}}=3$ ,

$u=-w\cdot q{\bmod {R}}=-64\cdot 3{\bmod {3}}2=-192{\bmod {3}}2=0$ ,

${\overline {z}}=(w+u\cdot N)/R=(64+0\cdot 32)/32=2$

Соответственно прообраз $z={\overline {z}}\cdot R^{-1}{\bmod {N}}=2\cdot 32^{-1}{\bmod {1}}1=9$

Применение

Данный метод дает выигрыш в производительности по сравнению с методом повторяющихся возведения в квадрат и умножения, так как умножение двух чисел по модулю происходит значительно быстрее.

Вычислительная сложность

Данный метод позволяет уменьшить (при больших значения $N$ ) вычисления функции $\operatorname {mod}$ до одного умножения двух чисел размером $N$ . Сложность умножения Монтгомери оценивается как $O(n^{2})$ .

Алгоритм с использованием «школьного» метода

Описание метода

Для наглядности рассмотрим метод для основания $B=2$ , то есть будем проводить вычисления в $B$ — ичной (или двоичной, так как $B=2$ ) системе счисления. Основание $B=2$ имеет плюс, в том что выполнение операции деления на $2$ происходит сдвигом вправо, а умножение на $2$ — сдвигом влево.

Определение 1. Представлением неотрицательного целого числа $x$ в системе счисления с основанием $B$ (или $B$ -ичной записью числа $x$ ) называется кратчайшая последовательность целых чисел $(x_{i})$ , называемых цифрами записи, такая что каждая из этих цифр удовлетворяет неравенству $0\leqslant x_{i}<B$ , и выполнено равенство $x=\sum _{i=0}^{D-1}x_{i}B^{i}$

Для примера, рассмотрим двоичный алгоритм взятия $\operatorname {mod}$ от произведения $xy$ .

Алгоритм (двоичный алгоритм умножения и взятия остатка). Пусть заданы положительные целые числа $x$ , $y$ такие что $0\leqslant x$ , $y<N$ . Этот алгоритм возвращает результат составной операции $(xy){\bmod {N}}$ . Мы предполагаем, что задано двоичное представление числа $x$ согласно определению 1, так что биты числа $x$ имеют вид $(x_{0},...,x_{D-1})$ , и $x_{D-1}>0$ — самый старший бит.

1.[Начальная установка]

s=0

;

2.[Преобразовать все

D

битов]

for

(D-1\geqslant j\geqslant 0)

{

s=2s

;

if

(s\geqslant N)s=s-N

;

if

(x_{j}==1)s=s+y

;

if

(s\geqslant N)s=s-N

;

}

return

s

;

Данный метод имеет один недостаток: он не использует преимущество многобитовой арифметики, доступной на любой современной ЭВМ. Поэтому обычно используют основания $B$ большие $2$ .

Вычислительная сложность «школьного» метода

Выражения вида $a^{b}({\bmod {n}})$ имеет оценку вычислительной сложности — $O_{s}((\log n)^{3})$

См. также

Примечания

Литература

Крэндалл Ричард, Померанс Карл. Простые числа: Криптографические и вычислительные аспекты / Под ред. и с предисл. В. Н. Чубарикова.. — М.: УРСС:: Книжный Дом «ЛИБРОКОМ», 2011. — 664 с. — ISBN 978-5-453-00016-6, 978-5-397-03060-2.
Молдовян Н. А. Теоретический минимум и алгоритмы цифровой подписи. — СПб.: БВХ-Петербург: Книжный Дом «ЛИБРОКОМ», 2010. — 304 с. — ISBN 978-5-9775-0585-7.
Фергюнсон, Нильс, Шнайер, Брюс. Практическая криптография. — M.: Издательский дом «Вильямс», 2004. — 432 с. — ISBN 5-8459-0733-0.
Мао В. Современная криптография: Теория и практика / пер. Д. А. Клюшина — М.: Вильямс, 2005. — 768 с. — ISBN 978-5-8459-0847-6

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.